Lt (x→1) (x^n - n) / (x - 1 - log(x))
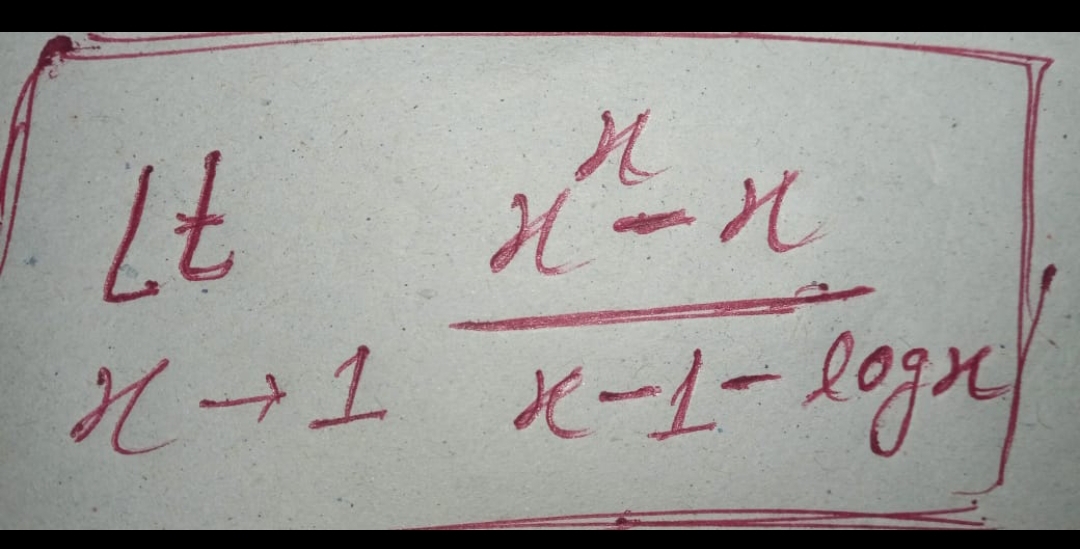
Understand the Problem
The question is asking to find the limit of the expression as x approaches 1. Specifically, it involves evaluating the limit of (x^n - n) / (x - 1 - log(x)) as x approaches 1.
Answer
The limit is \( n(n-1) \).
Answer for screen readers
The limit is
$$ n(n-1) $$.
Steps to Solve
- Direct Substitution
Start by substituting ( x = 1 ) into the expression.
$$ \frac{(1^n - n)}{(1 - 1 - \log(1))} = \frac{(1 - n)}{(0)} $$
This results in an indeterminate form of type ( \frac{0}{0} ).
- Apply L'Hôpital's Rule
Since we have the indeterminate form ( \frac{0}{0} ), we can apply L'Hôpital's Rule, which states we can take the derivative of the numerator and the derivative of the denominator.
- Differentiate Numerator and Denominator
Differentiate the numerator ( x^n - n ):
$$ \frac{d}{dx}(x^n - n) = nx^{n-1} $$
Differentiate the denominator ( x - 1 - \log(x) ):
$$ \frac{d}{dx}(x - 1 - \log(x)) = 1 - \frac{1}{x} $$
- Substitute Again
Now substitute ( x = 1 ) again after differentiating:
Numerator:
$$ n(1)^{n-1} = n $$
Denominator:
$$ 1 - \frac{1}{1} = 0 $$
Again, we have ( \frac{n}{0} ). Thus, we should apply L'Hôpital's Rule one more time.
- Differentiate Again
Differentiate the new numerator ( nx^{n-1} ):
$$ \frac{d}{dx}(nx^{n-1}) = n(n-1)x^{n-2} $$
Differentiate the new denominator ( 1 - \frac{1}{x} ):
$$ \frac{d}{dx}(1 - \frac{1}{x}) = \frac{1}{x^2} $$
- Final Substitution
Substituting ( x = 1 ) again:
Numerator:
$$ n(n-1)(1)^{n-2} = n(n-1) $$
Denominator:
$$ \frac{1}{1^2} = 1 $$
Thus,
$$ \lim_{x \to 1} \frac{nx^{n-1}}{1 - \frac{1}{x}} = n(n-1) $$
The limit is
$$ n(n-1) $$.
More Information
This limit evaluates the behavior of the function as ( x ) approaches 1. The application of L'Hôpital's Rule is vital in resolving the indeterminate forms that arise during the computation.
Tips
- Failing to recognize an indeterminate form when substituting values, especially ( \frac{0}{0} ).
- Not applying L'Hôpital's Rule correctly the second time if the first differentiation yields another indeterminate form.
- Confusing the differentiation of ( \log(x) ); it's essential to remember that the derivative is ( \frac{1}{x} ).
AI-generated content may contain errors. Please verify critical information