List the side lengths from shortest to longest for each triangle.
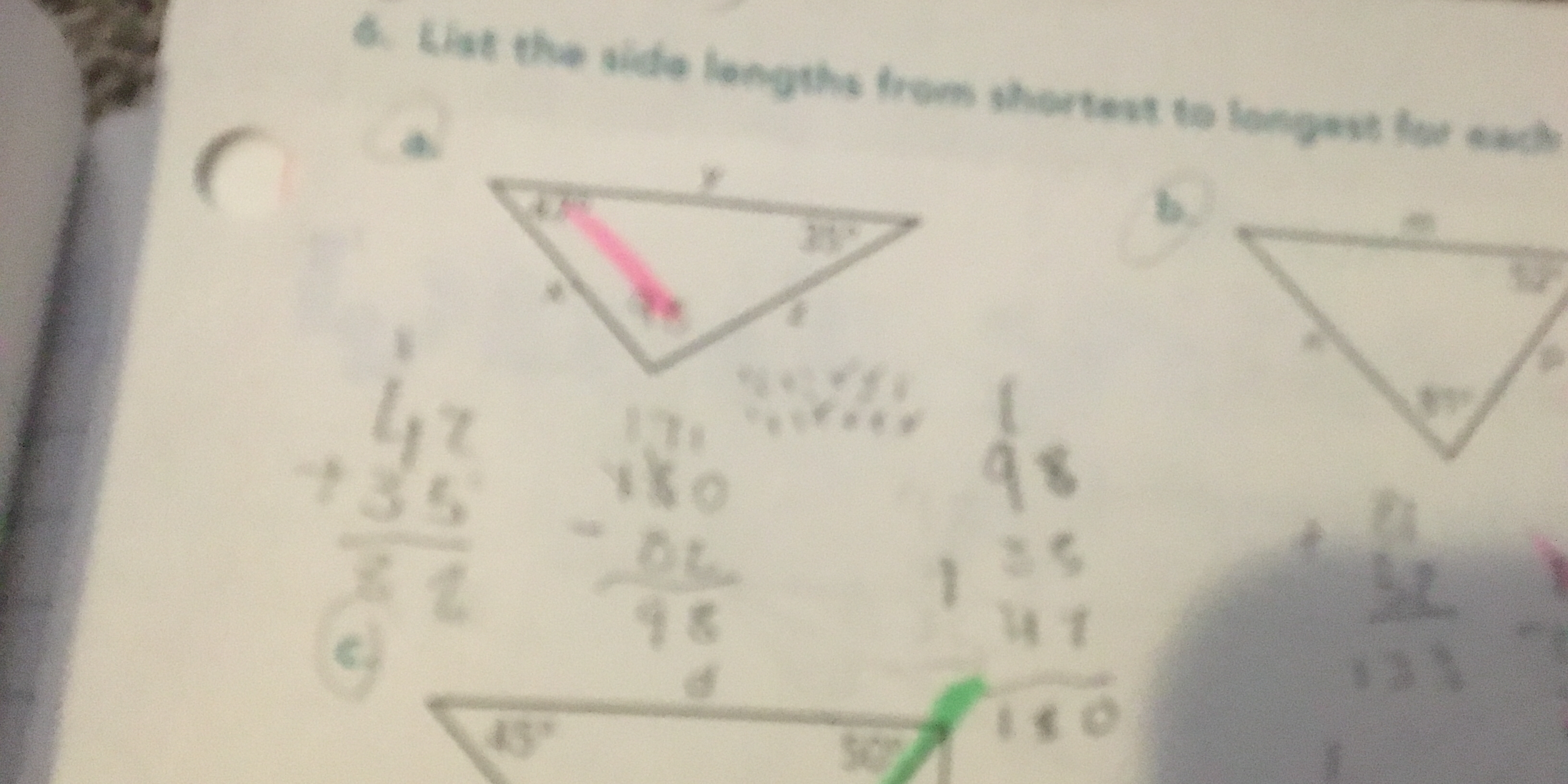
Understand the Problem
The question asks to list the side lengths of different triangles from shortest to longest. This requires using the angles provided in the triangles to infer the order of the sides, based on the relationship that larger angles are opposite longer sides.
Answer
a. $y, z, x$ b. $m, l, n$ c. $f, e, d$
Answer for screen readers
a. $y, z, x$ b. $m, l, n$ c. $f, e, d$
Steps to Solve
- Triangle a: Find the missing angle
The sum of the angles in a triangle is 180 degrees. Let the missing angle be $x$. $$ 47 + 35 + x = 180 $$ $$ 82 + x = 180 $$ $$ x = 180 - 82 = 98 $$ So, the angles are $35^\circ$, $47^\circ$, and $98^\circ$.
- Triangle a: Order the side lengths
The side opposite the largest angle is the longest, and the side opposite the smallest angle is the shortest. The angles in increasing order are $35^\circ$, $47^\circ$, $98^\circ$. The sides opposite these angles are $y$, $z$, and $x$, respectively. Therefore, the side lengths from shortest to longest are $y, z, x$.
- Triangle b: Find the missing angle
The sum of the angles in a triangle is 180 degrees. Let the missing angle be $x$. $$ 88 + 52 + x = 180 $$ $$ 140 + x = 180 $$ $$ x = 180 - 140 = 40 $$ So, the angles are $40^\circ$, $52^\circ$, and $88^\circ$.
- Triangle b: Order the side lengths
The angles in increasing order are $40^\circ$, $52^\circ$, $88^\circ$. The sides opposite these angles are $m$, $l$, and $n$, respectively. Therefore, the side lengths from shortest to longest are $m, l, n$.
- Triangle c: Find the missing angle
The sum of the angles in a triangle is 180 degrees. Let the missing angle be $x$. $$ 45 + 50 + x = 180 $$ $$ 95 + x = 180 $$ $$ x = 180 - 95 = 85 $$ So, the angles are $45^\circ$, $50^\circ$, and $85^\circ$.
- Triangle c: Order the side lengths
The angles in increasing order are $45^\circ$, $50^\circ$, $85^\circ$. The sides opposite these angles are $f$, $e$, and $d$, respectively. Therefore, the side lengths from shortest to longest are $f, e, d$.
a. $y, z, x$ b. $m, l, n$ c. $f, e, d$
More Information
In a triangle, the longest side is always opposite the largest angle, and the shortest side is always opposite the smallest angle.
Tips
A common mistake is to assume that the order of the sides corresponds directly to the "order" they appear in the diagram, without considering the angles opposite them. Also, one might forget to calculate the missing angle in the triangle before ordering the sides.
AI-generated content may contain errors. Please verify critical information