lim n → 0 (1 - sin(n)) / cos(n)
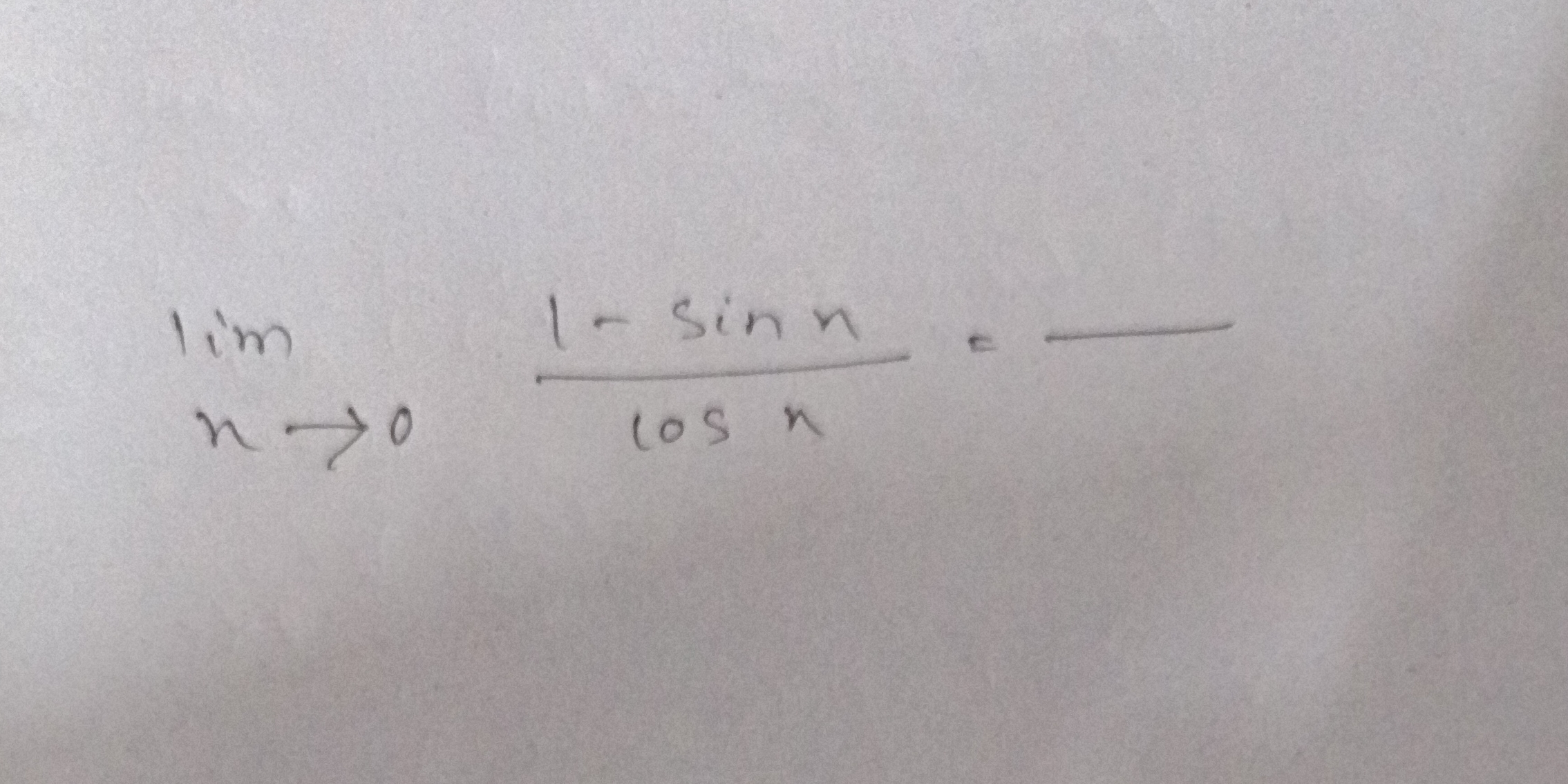
Understand the Problem
The question involves finding the limit of the expression (1 - sin(n)) / cos(n) as n approaches 0. This indicates a calculus problem dealing with limits and trigonometric functions.
Answer
The limit is: \( 1 \)
Answer for screen readers
The limit is:
$$ 1 $$
Steps to Solve
-
Identify the limit expression
We need to evaluate the limit:
$$ \lim_{n \to 0} \frac{1 - \sin(n)}{\cos(n)} $$ -
Substitute the limit directly
First, we can substitute ( n = 0 ) into the expression:
$$ \frac{1 - \sin(0)}{\cos(0)} = \frac{1 - 0}{1} = \frac{1}{1} = 1 $$ -
Check for indeterminate form
Since ( \sin(0) = 0 ) and ( \cos(0) = 1 ), the limit does not yield an indeterminate form. Thus, we can confirm that the direct substitution gives us a valid result.
The limit is:
$$ 1 $$
More Information
The limit represents the value that the function approaches as ( n ) gets closer to zero. The trigonometric functions ( \sin(n) ) and ( \cos(n) ) are fundamental in calculus, and their values at specific points (like zero) are often used in limit evaluations.
Tips
- Not recognizing when to directly substitute values into a limit expression. It's essential to check if the expression is defined at the limit point.
- Assuming that the limit always exists without verifying the form of the function at the limit point.
AI-generated content may contain errors. Please verify critical information