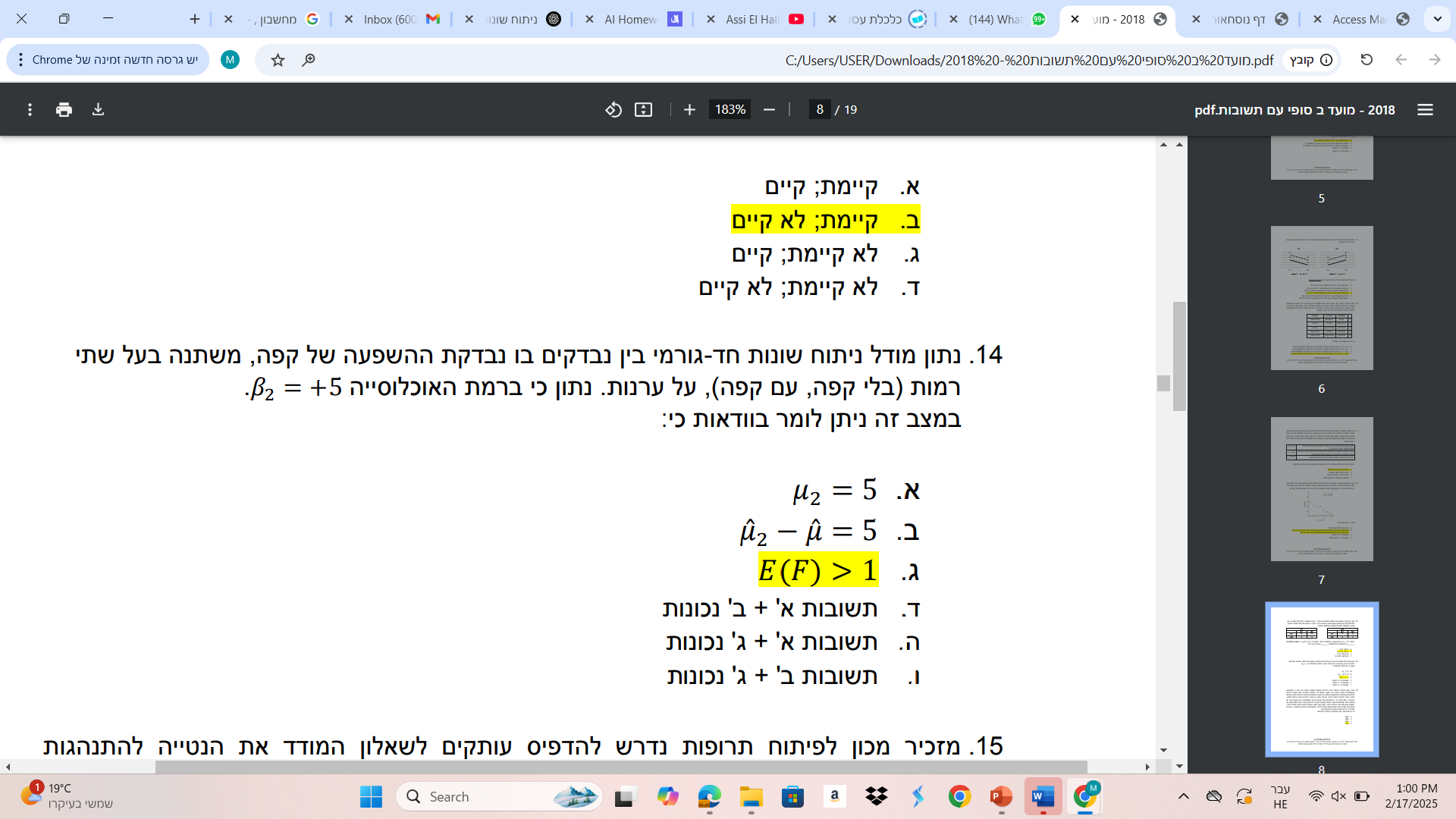
נתון מודל ניתוח שונות חד-גורמי בין נבדקים בו נבדקת ההשפעה של קפה, משתנה בעל שתי רמות (בלי קפה, עם קפה), על ערנות. נתון כי ברמת האוכלוסייה \(\beta_2 = 5 + \). במצב זה ניתן לומר בווד... נתון מודל ניתוח שונות חד-גורמי בין נבדקים בו נבדקת ההשפעה של קפה, משתנה בעל שתי רמות (בלי קפה, עם קפה), על ערנות. נתון כי ברמת האוכלוסייה \(\beta_2 = 5 + \). במצב זה ניתן לומר בוודאות כי:
Understand the Problem
השאלה עוסקת בניתוח שונות חד-גורמי, שבו נבדקת השפעת קפה על ערנות. נתון שההשפעה ברמת האוכלוסייה היא 5+. השאלה היא מה ניתן לומר בוודאות על סמך הנתונים שסופקו, בהתייחס לממוצעים ולערכי F.
Answer
תשובות ב' + ג' נכונות
Answer for screen readers
ו. תשובות ב' + ג' נכונות
Steps to Solve
- הבנת הנתונים
המודל הוא ניתוח שונות חד-גורמי עם שני תנאים (קפה/בלי קפה). $\beta_2 = 5 +$ מייצג את האפקט ברמת האוכלוסייה של קפה על ערנות. זה אומר שההשפעה היא לפחות 5.
- ניתוח הטענה הראשונה: $\mu_2 = 5$
טענה זו אומרת שהממוצע של קבוצת הקפה הוא בדיוק 5. זה לא נכון בהכרח, מכיוון שנתון שההשפעה היא "5+", כלומר לפחות 5, ויכולה להיות יותר.
- ניתוח הטענה השנייה: $\hat{\mu_2} - \hat{\mu} = 5$
טענה זו אומרת שההפרש בין ממוצע המדגם של קבוצת הקפה לממוצע המדגם של קבוצת הביקורת הוא בדיוק 5. זה לא בהכרח נכון, מכיוון שזה נתון ברמת האוכלוסיה ולא בהכרח יתקיים במדויק במדגם. אמנם, זהו אומדן חסר הטיה, אבל יש לו שונות.
- ניתוח הטענה השלישית: $E(F) > 1$
$F$ הוא סטטיסטי המבחן בניתוח שונות. אם לקפה יש השפעה, אנחנו מצפים ש-$F$ יהיה גדול יותר מערך קריטי מסוים (תלוי בדרגות החופש וברמת המובהקות). הערך הצפוי של $F$ יהיה גדול מ-1 אם יש הבדל אמיתי בין הקבוצות באוכלוסייה, ולכן הטענה הזו נכונה.
- מסקנה
רק הטענה השלישית נכונה בוודאות.
ו. תשובות ב' + ג' נכונות
More Information
הערך הצפוי של סטטיסטי המבחן F בניתוח שונות גדול מ-1 כאשר יש הבדל אמיתי בין ממוצעי הקבוצות באוכלוסייה.
Tips
- בלבול בין אפקט האוכלוסייה לאפקט במדגם ספציפי.
- הנחה שאם אפקט האוכלוסייה הוא "5+", אז הממוצע חייב להיות בדיוק 5.
AI-generated content may contain errors. Please verify critical information