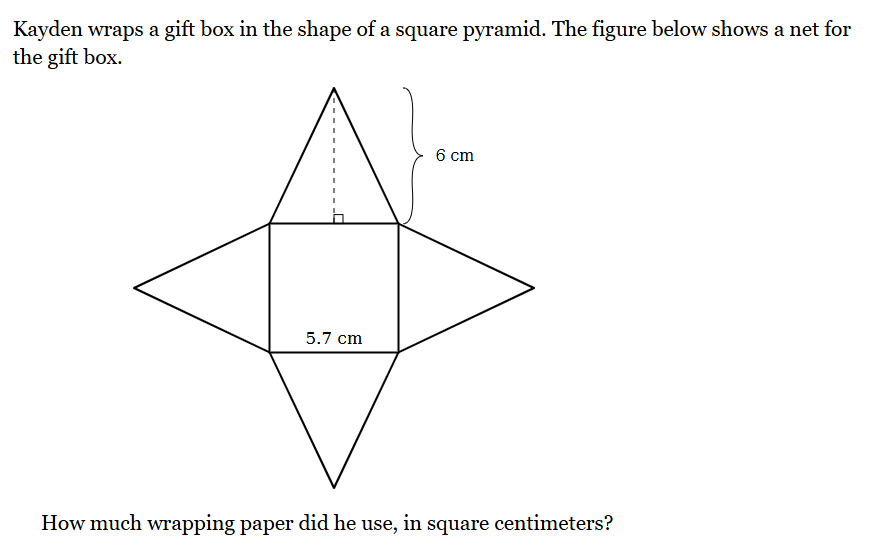
Kayden wraps a gift box in the shape of a square pyramid. The figure below shows a net for the gift box. How much wrapping paper did he use, in square centimeters?
Understand the Problem
The question asks to calculate the surface area of a square pyramid given its net. The net consists of a square and four congruent triangles. We need to find the areas of the square and the triangles and add them together to determine the total amount of wrapping paper used.
Answer
$100.89 \text{ cm}^2$
Answer for screen readers
$100.89 \text{ cm}^2$
Steps to Solve
- Calculate the area of the square
The side length of the square is given as 5.7 cm. The area of a square is side length squared.
$$Area_{square} = (5.7 \text{ cm})^2 = 32.49 \text{ cm}^2$$
- Calculate the area of one triangle
The base of each triangle is the same as the side of the square, which is 5.7 cm. The height of each triangle is given as 6 cm. The area of a triangle is $1/2 \times base \times height$.
$$Area_{triangle} = \frac{1}{2} \times 5.7 \text{ cm} \times 6 \text{ cm} = 17.1 \text{ cm}^2$$
- Calculate the total area of the four triangles
Since there are four congruent triangles, multiply the area of one triangle by 4. $$Area_{4 triangles} = 4 \times 17.1 \text{ cm}^2 = 68.4 \text{ cm}^2$$
- Calculate the total surface area
Add the area of the square and the total area of the four triangles. $$Total \ Area = Area_{square} + Area_{4 triangles} = 32.49 \text{ cm}^2 + 68.4 \text{ cm}^2 = 100.89 \text{ cm}^2$$
$100.89 \text{ cm}^2$
More Information
The surface area represents the total amount of wrapping paper Kayden used to cover the gift box.
Tips
A common mistake is forgetting to multiply the area of a single triangle by 4 to account for all four triangles in the net. Also, errors can occur in the arithmetic calculations, especially when squaring the side length of the square or multiplying the triangle's base and height.
AI-generated content may contain errors. Please verify critical information