Is this shape a regular polygon?
Understand the Problem
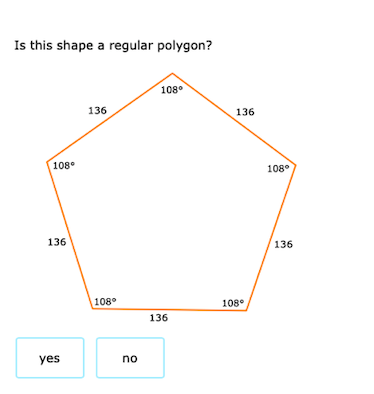
The question is asking whether the given shape, which is a hexagon with specified interior angles, qualifies as a regular polygon. A regular polygon has all sides and angles equal.
Answer
No, this shape is not a regular polygon.
Answer for screen readers
No, this shape is not a regular polygon.
Steps to Solve
- Identify the angles of the hexagon
The given hexagon has the following angles: $136^\circ$, $136^\circ$, $108^\circ$, $136^\circ$, $108^\circ$, and $136^\circ$.
- Count the equal angles
Observe the angles. In a regular polygon, all interior angles must be equal. Here, we see that $136^\circ$ appears four times, and $108^\circ$ appears twice. Hence, they are not all equal.
- Conclusion about regularity
Since not all angles are equal, this hexagon cannot be classified as a regular polygon.
No, this shape is not a regular polygon.
More Information
A regular hexagon has all angles measuring $120^\circ$. In this case, the angles vary, confirming that the shape does not have uniformity in its angles.
Tips
Common mistakes include:
- Assuming a polygon is regular if it has equal sides, without checking the angles.
- Overlooking the requirement for both angles and sides to be equal.
AI-generated content may contain errors. Please verify critical information