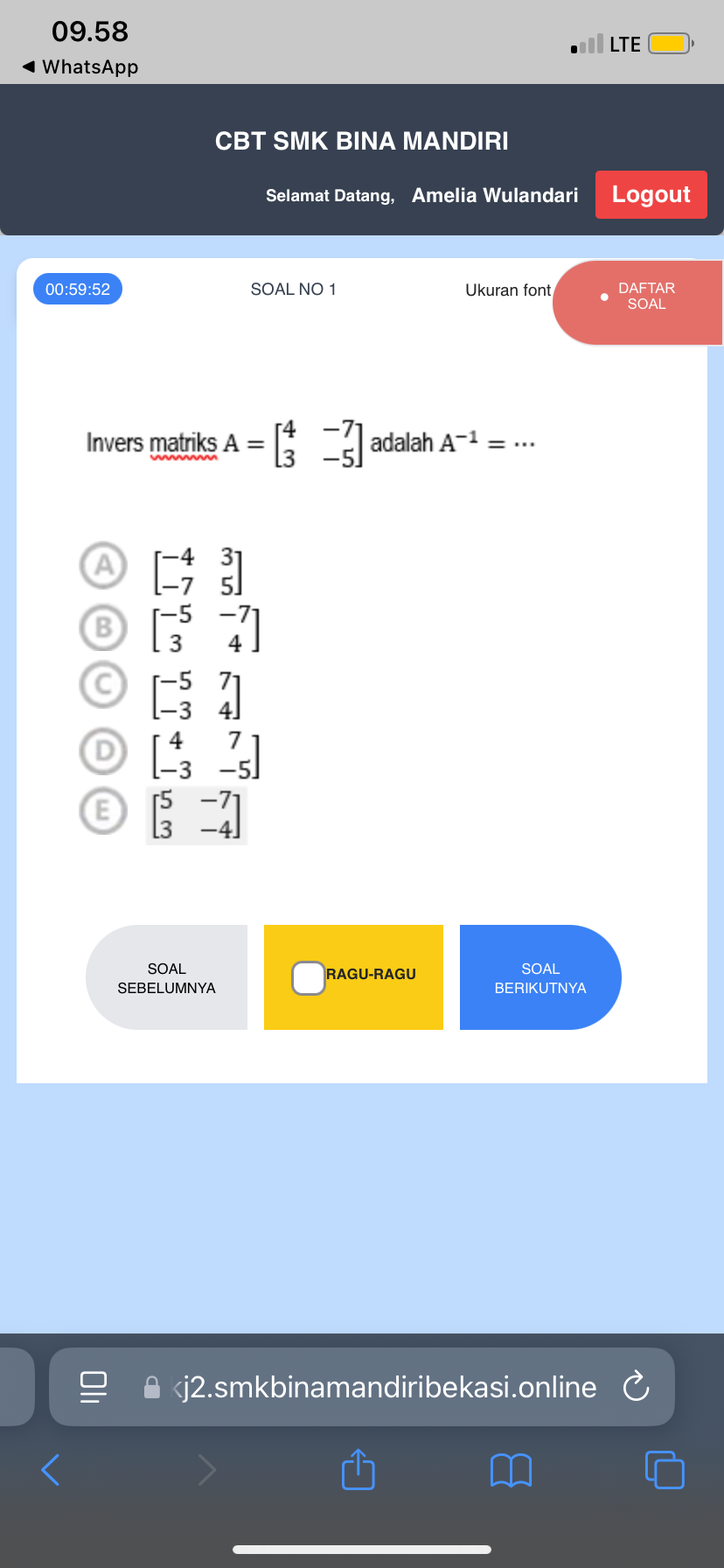
Invers matriks A = [[4, -7], [3, -5]] adalah A⁻¹ = ...
Understand the Problem
Pertanyaan ini meminta kita untuk menentukan invers dari matriks A yang diberikan. Matriks yang diberikan adalah [[4, -7], [3, -5]] dan kita perlu mencari A⁻¹ dari matriks ini. Kita harus menggunakan rumus invers matriks untuk melakukan perhitungan.
Answer
$$ A^{-1} = \begin{bmatrix} -5 & 7 \\ -3 & 4 \end{bmatrix} $$
Answer for screen readers
$$ A^{-1} = \begin{bmatrix} -5 & 7 \ -3 & 4 \end{bmatrix} $$
Steps to Solve
- Menentukan Determinan Matriks A
Untuk menghitung invers dari matriks, kita perlu menemukan determinan dari matriks A. Matriks A diberikan sebagai: $$ A = \begin{bmatrix} 4 & -7 \ 3 & -5 \end{bmatrix} $$
Rumus untuk menentukan determinan dari matriks 2x2 adalah: $$ \text{det}(A) = ad - bc $$
Di sini, $a = 4$, $b = -7$, $c = 3$, dan $d = -5$.
Menentukan determinan: $$ \text{det}(A) = (4 \cdot -5) - (-7 \cdot 3) = -20 + 21 = 1 $$
- Menghitung Invers Matriks A
Setelah kita mendapatkan determinan, kita menggunakan rumus invers dari matriks 2x2: $$ A^{-1} = \frac{1}{\text{det}(A)} \begin{bmatrix} d & -b \ -c & a \end{bmatrix} $$
Dengan substitusi nilai ke dalam rumus: $$ A^{-1} = \frac{1}{1} \begin{bmatrix} -5 & 7 \ -3 & 4 \end{bmatrix} $$
- Kesimpulan Invers Matriks A
Matriks invers A yang kita dapatkan adalah: $$ A^{-1} = \begin{bmatrix} -5 & 7 \ -3 & 4 \end{bmatrix} $$
$$ A^{-1} = \begin{bmatrix} -5 & 7 \ -3 & 4 \end{bmatrix} $$
More Information
Invers dari suatu matriks sangat penting dalam banyak aplikasi matematika dan teknik, termasuk pemecahan sistem persamaan linear.
Tips
- Lupa menghitung determinan dengan benar yang bisa menyebabkan kesalahan dalam invers.
- Salah menempatkan elemen-elemen dalam matriks invers.
AI-generated content may contain errors. Please verify critical information