Integrate (x² + 4x³ + 2) / (6x) dx
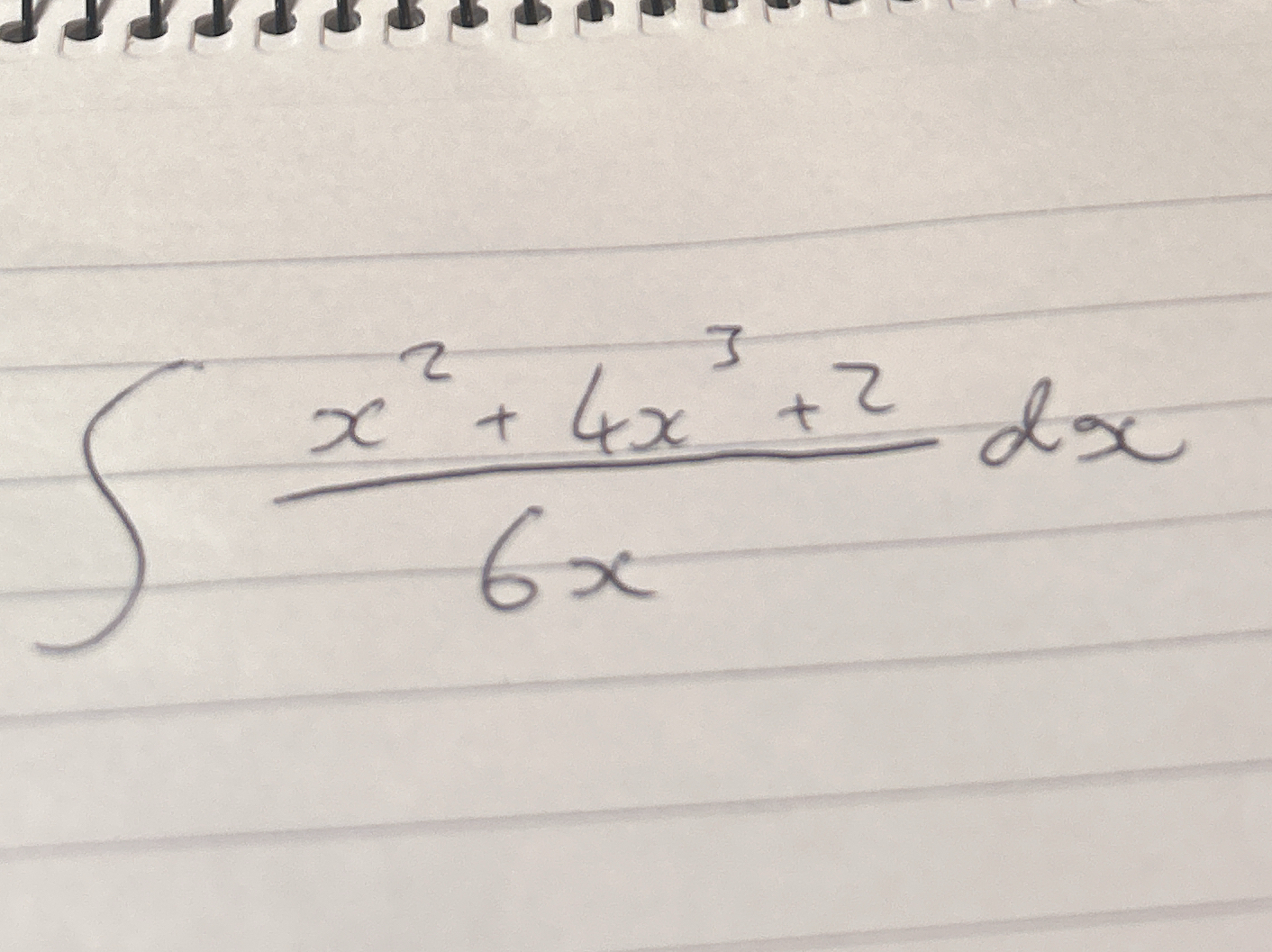
Understand the Problem
The question is asking to compute the integral of a rational function, specifically the integral of (x² + 4x³ + 2) / (6x) with respect to x.
Answer
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
Answer for screen readers
$$ \int \frac{x^2 + 4x^3 + 2}{6x} , dx = \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
Steps to Solve
-
Rewrite the Rational Function
We can simplify the integral by dividing each term in the numerator by the denominator. The function becomes:
$$ \int \frac{x^2}{6x} + \frac{4x^3}{6x} + \frac{2}{6x} , dx $$
Which simplifies to:
$$ \int \frac{x}{6} + \frac{2}{3}x^2 + \frac{1}{3x} , dx $$ -
Separate the Integral
Next, we can separate the integral into individual terms:
$$ \int \left( \frac{x}{6} + \frac{2}{3} x^2 + \frac{1}{3x} \right) , dx = \frac{1}{6} \int x , dx + \frac{2}{3} \int x^2 , dx + \frac{1}{3} \int \frac{1}{x} , dx $$ -
Integrate Each Term
Now we will integrate each term individually:
- For the first term:
$$ \int x , dx = \frac{x^2}{2} $$ - For the second term:
$$ \int x^2 , dx = \frac{x^3}{3} $$ - For the third term:
$$ \int \frac{1}{x} , dx = \ln |x| $$
-
Combine the Results
Now, substituting back into our equation: $$ \frac{1}{6} \cdot \frac{x^2}{2} + \frac{2}{3} \cdot \frac{x^3}{3} + \frac{1}{3} \ln |x| + C $$ This simplifies to:
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$ -
Final Result
The final result of the integral is:
$$ \int \frac{x^2 + 4x^3 + 2}{6x} , dx = \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
$$ \int \frac{x^2 + 4x^3 + 2}{6x} , dx = \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
More Information
This integral simplifies multiple rational functions, showcasing the use of basic integration techniques and properties of logarithms. The integration of fractions can lead to logarithmic expressions, especially when dealing with terms like $\frac{1}{x}$.
Tips
- Forgetting to simplify the rational function before integrating can make the process unnecessarily complicated.
- Misapplying the rules of integration, especially for logarithmic functions.
- Not including the constant of integration ($C$) at the end.
AI-generated content may contain errors. Please verify critical information