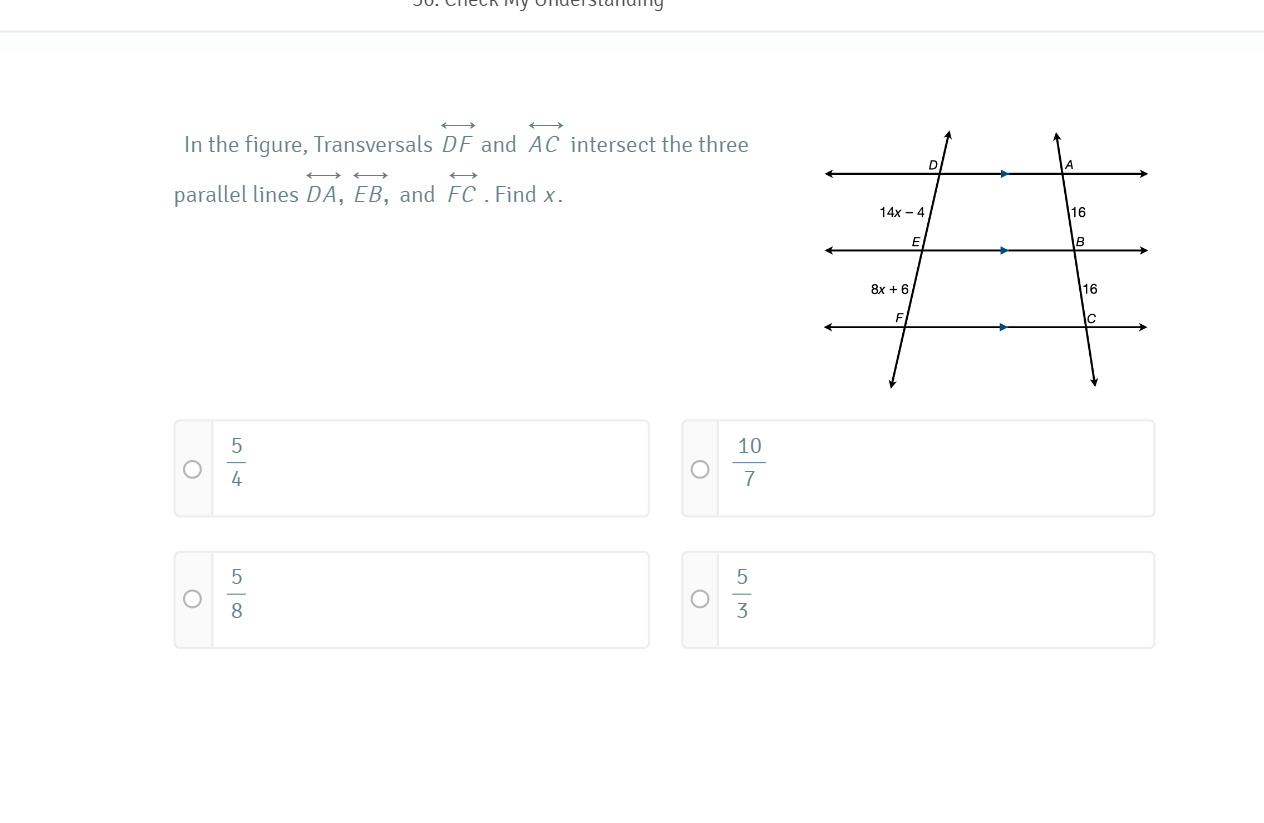
In the figure, transversals DF and AC intersect the three parallel lines DA, EB, and FC. Find x.
Understand the Problem
The question involves finding the value of x in a geometric figure where two transversals intersect three parallel lines. It requires applying properties of angles formed by transversals and parallel lines.
Answer
The value of $x$ is \( \frac{10}{7} \).
Answer for screen readers
The value of $x$ is ( \frac{10}{7} ).
Steps to Solve
-
Identify the Angles Formed by the Transversals
In the given figure, the transversals $DF$ and $AC$ intersect the parallel lines $DA$, $EB$, and $FC$. The angles formed at intersections create corresponding angles that are equal.
-
Set Up the Equation from Corresponding Angles
The angle labeled $14x - 4$ and the angle labeled $16$ at line $EB$ are corresponding angles. Therefore, we can set up the equation: $$ 14x - 4 = 16 $$
-
Solve for x
To find $x$, we need to solve the equation from the previous step:
- Add 4 to both sides: $$ 14x = 20 $$
- Divide both sides by 14: $$ x = \frac{20}{14} $$
- Simplify the fraction: $$ x = \frac{10}{7} $$
-
Verification
We can verify by substituting $x$ back into the angle expressions to confirm they are equal:
- Calculate $14x - 4$: $$ 14 \cdot \frac{10}{7} - 4 = 20 - 4 = 16 $$
- Since both corresponding angles equal 16, our solution is correct.
The value of $x$ is ( \frac{10}{7} ).
More Information
This problem illustrates the properties of corresponding angles formed by transversals intersecting parallel lines, a fundamental concept in geometry.
Tips
- Confusing corresponding angles with alternate interior angles; remember they have different properties.
- Forgetting to simplify fractions; always check if your answer can be reduced.
AI-generated content may contain errors. Please verify critical information