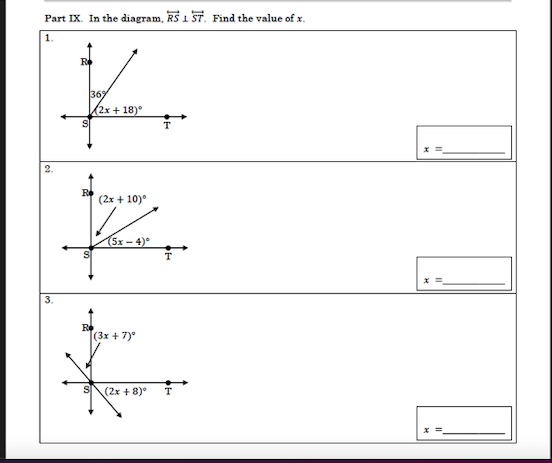
In the diagram, R5 is parallel to S7. Find the value of x for the following equations involving angles: 1. (2x + 18)° + 36° = 180 2. (2x + 10)° + (5x - 4)° = 180 3. (3x + 7)° + (2x... In the diagram, R5 is parallel to S7. Find the value of x for the following equations involving angles: 1. (2x + 18)° + 36° = 180 2. (2x + 10)° + (5x - 4)° = 180 3. (3x + 7)° + (2x + 8)° = 180
Understand the Problem
The question is asking to find the value of 'x' in three different equations that relate to angles formed by intersecting lines, leveraging properties of angles such as complementary or supplementary angles.
Answer
1. \( x = 63 \) 2. \( x \approx 24.857 \) 3. \( x = 33 \)
Answer for screen readers
-
( x = 63 )
-
( x \approx 24.857 )
-
( x = 33 )
Steps to Solve
-
Identify Relationships Between Angles In the given diagrams, we recognize that the pair of angles formed are either supplementary or complementary. Supplementary angles add up to (180^\circ).
-
Set Up the First Equation (Problem 1) For the first equation, (36^\circ) and ((2x + 18)^\circ) are supplementary: [ 36 + (2x + 18) = 180 ]
-
Simplify and Solve for x (Problem 1) Combine like terms: [ 36 + 2x + 18 = 180 ] [ 2x + 54 = 180 ] Subtract (54) from both sides: [ 2x = 126 ] Divide by (2): [ x = 63 ]
-
Set Up the Second Equation (Problem 2) For the second equation, ((2x + 10)^\circ) and ((5x - 4)^\circ) are supplementary: [ (2x + 10) + (5x - 4) = 180 ]
-
Simplify and Solve for x (Problem 2) Combine like terms: [ 2x + 10 + 5x - 4 = 180 ] [ 7x + 6 = 180 ] Subtract (6) from both sides: [ 7x = 174 ] Divide by (7): [ x = 24.857 \text{ (rounded to three decimal places)} ]
-
Set Up the Third Equation (Problem 3) For the third equation, ((3x + 7)^\circ) and ((2x + 8)^\circ) are supplementary: [ (3x + 7) + (2x + 8) = 180 ]
-
Simplify and Solve for x (Problem 3) Combine like terms: [ 3x + 7 + 2x + 8 = 180 ] [ 5x + 15 = 180 ] Subtract (15) from both sides: [ 5x = 165 ] Divide by (5): [ x = 33 ]
-
( x = 63 )
-
( x \approx 24.857 )
-
( x = 33 )
More Information
- The values of (x) are found using properties of supplementary angles.
- In the first problem, we used basic algebra to isolate (x).
- The second problem required careful simplification to avoid errors when combining terms.
Tips
- Forgetting that supplementary angles sum to (180^\circ).
- Miscalculating the simplification, especially when combining like terms.
- Not checking the final result by substituting back into the original equations.
AI-generated content may contain errors. Please verify critical information