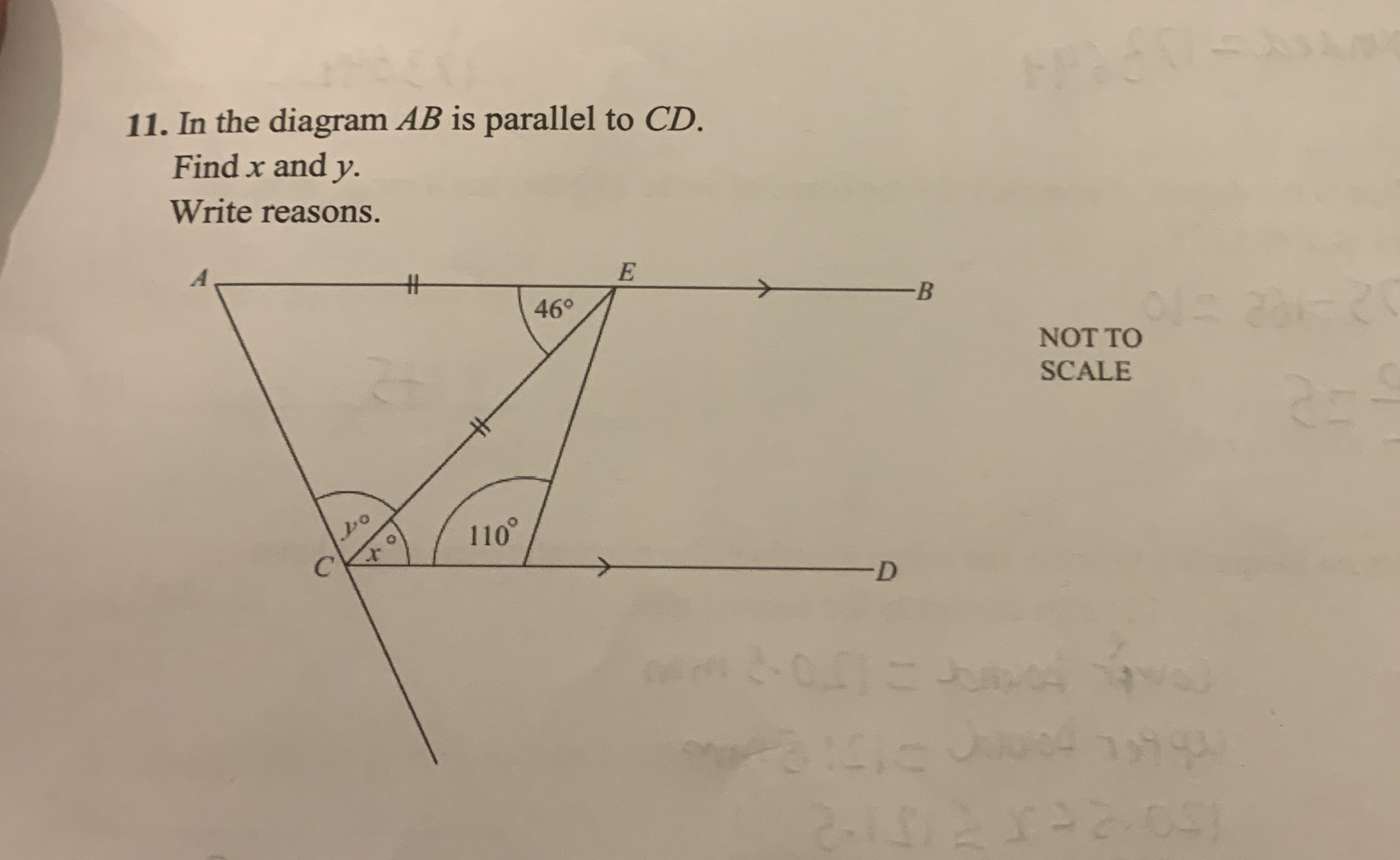
In the diagram AB is parallel to CD. Find x and y. Write reasons.
Understand the Problem
The question asks to find the values of x and y in a geometric diagram involving parallel lines and angles. The solution requires applying properties of angles formed when two lines intersect parallel lines, including alternate interior angles and corresponding angles.
Answer
\( x = 24° \), \( y = 46° \)
Answer for screen readers
The values are ( x = 24° ) and ( y = 46° ).
Steps to Solve
-
Identify the parallel lines and angles Given that ( AB ) is parallel to ( CD ), we can use the properties of angles formed by a transversal cutting through parallel lines. We focus on the angles 46°, 110°, ( x ), and ( y ).
-
Use corresponding angles The angle of 46° is corresponding to the angle above line ( CD ) that is labeled as ( y ). Therefore, we can conclude: $$ y = 46° $$
-
Use angle sum property Next, observe the triangle formed by angles ( x ), ( 110° ), and ( y ). The sum of angles in a triangle is 180°. Using this, we have: $$ x + 110° + y = 180° $$
-
Substitute ( y ) into the equation Now substitute ( y ) with its value from Step 2: $$ x + 110° + 46° = 180° $$
-
Combine the known angles Combining the known angles gives: $$ x + 156° = 180° $$
-
Solve for ( x ) Now isolate ( x ): $$ x = 180° - 156° $$ $$ x = 24° $$
The values are ( x = 24° ) and ( y = 46° ).
More Information
In this problem, we applied the properties of parallel lines and transversals, specifically the concept of corresponding angles and the sum of angles in a triangle.
Tips
- Misidentifying corresponding angles or failing to recognize their equality.
- Forgetting the angle sum property of triangles, which can lead to incorrect values for ( x ).
AI-generated content may contain errors. Please verify critical information