If y = √x, find dy/dx.
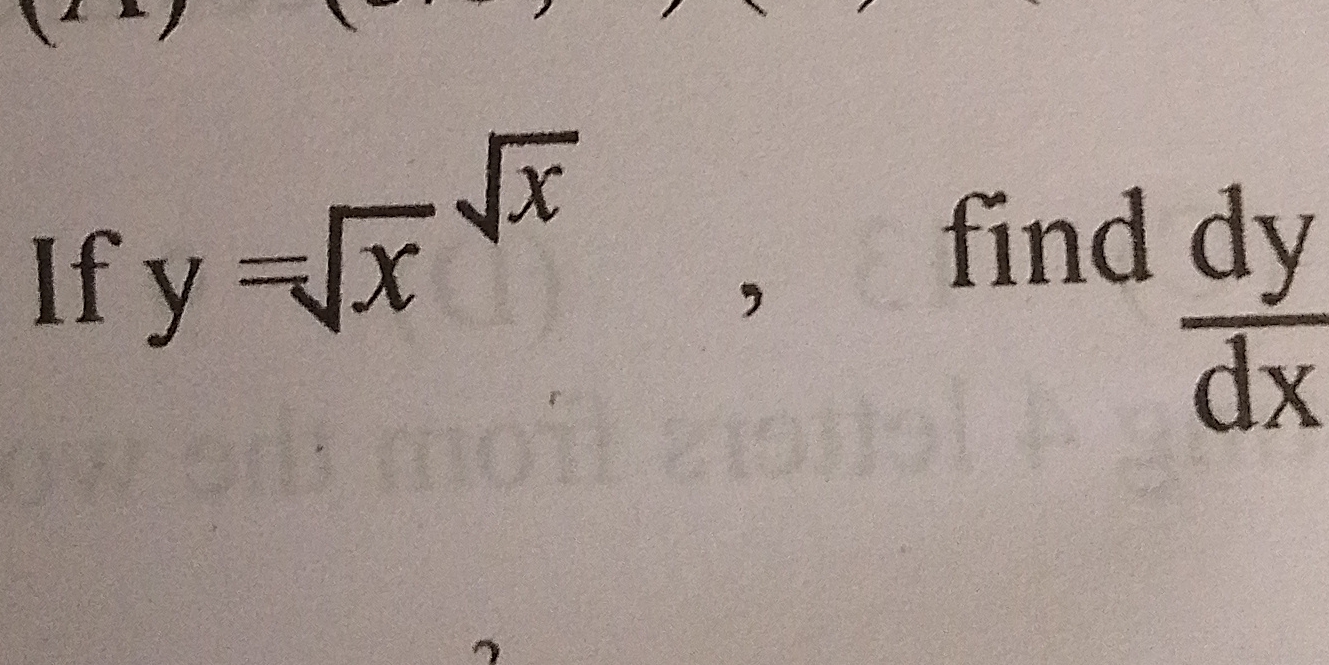
Understand the Problem
The question asks to find the derivative of the function y, which is defined as y = √x. The goal is to compute dy/dx using differentiation rules.
Answer
$$ \frac{dy}{dx} = \frac{1}{2\sqrt{x}} $$
Answer for screen readers
The derivative is
$$ \frac{dy}{dx} = \frac{1}{2\sqrt{x}} $$
Steps to Solve
- Rewrite the function for differentiation
The function ( y = \sqrt{x} ) can be rewritten in exponent form as:
$$ y = x^{1/2} $$
- Apply the power rule of differentiation
Using the power rule, which states that if ( y = x^n ), then ( \frac{dy}{dx} = n \cdot x^{n-1} ), we differentiate:
$$ \frac{dy}{dx} = \frac{1}{2} \cdot x^{\frac{1}{2} - 1} $$
- Simplify the derivative
Now simplify the expression:
$$ \frac{dy}{dx} = \frac{1}{2} \cdot x^{-\frac{1}{2}} $$
- Rewrite in radical form
To express ( x^{-\frac{1}{2}} ) in radical form:
$$ x^{-\frac{1}{2}} = \frac{1}{\sqrt{x}} $$
Thus, the derivative becomes:
$$ \frac{dy}{dx} = \frac{1}{2\sqrt{x}} $$
The derivative is
$$ \frac{dy}{dx} = \frac{1}{2\sqrt{x}} $$
More Information
This derivative tells us the rate at which ( y = \sqrt{x} ) changes with respect to ( x ). It is particularly useful in calculus to understand the behavior of the function, including its slope at any given point.
Tips
- Forgetting to rewrite the square root in exponent form before differentiating.
- Not applying the power rule correctly, especially forgetting to subtract one from the exponent.
- Confusing positive and negative exponents when rewriting expressions.
AI-generated content may contain errors. Please verify critical information