If y = √(secx - 1)/(secx + 1) then find the value of dy/dx.
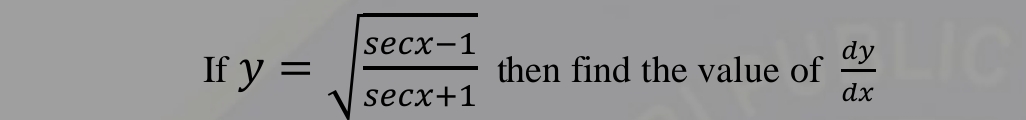
Understand the Problem
The question asks to find the derivative \( \frac{dy}{dx} \) of the function \( y = \sqrt{\frac{secx - 1}{secx + 1}} \). We need to differentiate this function using calculus techniques.
Answer
$$ \frac{\sec x \tan x}{\left(\sec x + 1\right)^2 \sqrt{\frac{\sec x - 1}{\sec x + 1}}} $$
Answer for screen readers
The value of ( \frac{dy}{dx} ) is
$$ \frac{\sec x \tan x}{\left(\sec x + 1\right)^2 \sqrt{\frac{\sec x - 1}{\sec x + 1}}} $$
Steps to Solve
- Identify the function to differentiate
We have the function given as $$ y = \sqrt{\frac{\sec x - 1}{\sec x + 1}} $$
- Apply the chain rule
To differentiate, we will use the chain rule, which states that if (y = f(g(x))), then $$ \frac{dy}{dx} = f'(g(x)) \cdot g'(x) $$ Here, let $$ u = \frac{\sec x - 1}{\sec x + 1} $$ Then (y = \sqrt{u}), and we need to find $$ \frac{dy}{dx} = \frac{1}{2\sqrt{u}} \cdot \frac{du}{dx} $$
- Differentiate (u)
Now, we will differentiate (u) using the quotient rule. The quotient rule states that $$ \frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x) - f(x)g'(x)}{(g(x))^2} $$
In our case, let (f(x) = \sec x - 1) and (g(x) = \sec x + 1):
- The derivative of (f(x)) is (f'(x) = \sec x \tan x)
- The derivative of (g(x)) is (g'(x) = \sec x \tan x)
So,
$$ \frac{du}{dx} = \frac{(\sec x \tan x)(\sec x + 1) - (\sec x - 1)(\sec x \tan x)}{(\sec x + 1)^2} $$
- Simplify (\frac{du}{dx})
After substituting and simplifying, we notice that $$ \frac{du}{dx} = \frac{\sec x \tan x \cdot 2}{(\sec x + 1)^2} $$
- Combine to find (\frac{dy}{dx})
Now substituting back into the equation for (\frac{dy}{dx}):
$$ \frac{dy}{dx} = \frac{1}{2\sqrt{u}} \cdot \frac{du}{dx} = \frac{1}{2\sqrt{\frac{\sec x - 1}{\sec x + 1}}} \cdot \frac{2 \sec x \tan x}{(\sec x + 1)^2} $$
After simplifying the terms, we get:
$$ \frac{dy}{dx} = \frac{\sec x \tan x}{\left(\sec x + 1\right)^2 \sqrt{\frac{\sec x - 1}{\sec x + 1}}} $$
The value of ( \frac{dy}{dx} ) is
$$ \frac{\sec x \tan x}{\left(\sec x + 1\right)^2 \sqrt{\frac{\sec x - 1}{\sec x + 1}}} $$
More Information
This derivative can be useful when analyzing the behavior of the function (y = \sqrt{\frac{\sec x - 1}{\sec x + 1}}), particularly in understanding its slope and the rate of change at various points on the graph.
Tips
One common mistake is neglecting to apply the chain rule correctly or misapplying the quotient rule. It's essential to carefully differentiate each part of the function and apply the rules correctly to avoid errors.
AI-generated content may contain errors. Please verify critical information