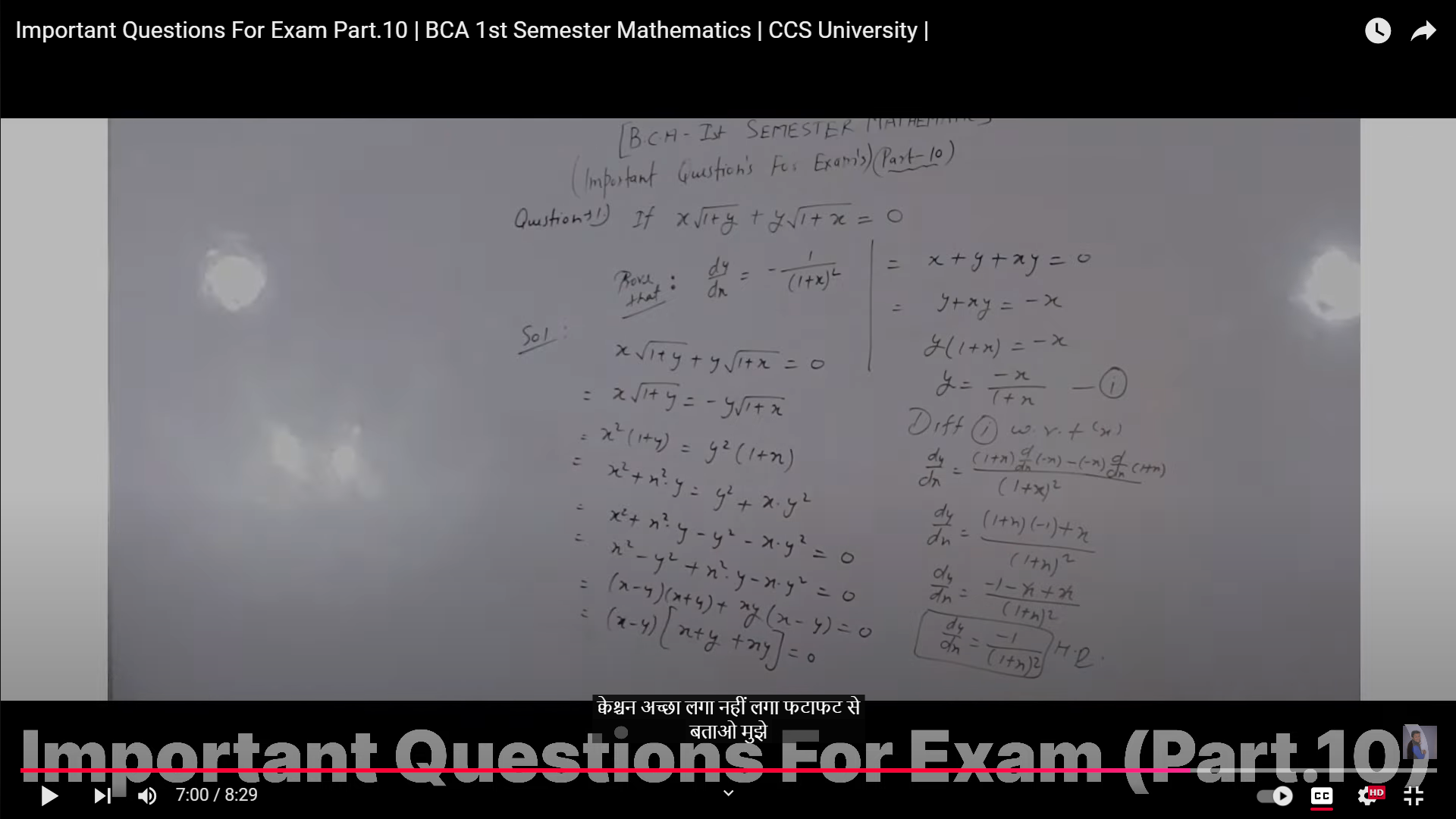
If x*y + y + x*y = 0, prove that dy/dn = -1/(1+x)^2.

Steps to Solve

1. Rewriting the Original Equation

   Start with the given equation: $$ x \cdot y + y + x \cdot y = 0 $$ This can be simplified to: $$ 2xy + y = 0 $$ Factoring out $y$ gives: $$ y(2x + 1) = 0 $$

2. Identifying Solutions for y

   Since $y(2x + 1) = 0$, we can deduce:

   • Either $y = 0$, which we want to ignore for differentiation,
   • Or $2x + 1 = 0 \implies x = -\frac{1}{2}$.

   Therefore, we need to focus on further transformations instead of a static solution.

3. Differentiating Implicitly

   Start from the original equation: $$ x \cdot y + y + x \cdot y = 0 $$ Differentiate with respect to $n$.

   Using the product rule on (xy): $$ \frac{d}{dn}(xy) = x \frac{dy}{dn} + y \frac{dx}{dn} $$

4. Applying Differentiation

   Differentiate the entire equation: $$ \frac{d}{dn}(xy + y + xy) = 0 $$ yields: $$ x \frac{dy}{dn} + y \frac{dx}{dn} + \frac{dy}{dn} + x \frac{dy}{dn} = 0 $$

5. Simplifying the Derivative Expression

   Combine like terms: $$ (x + 1 + x) \frac{dy}{dn} + y\frac{dx}{dn} = 0 $$ This simplifies to: $$ (2x + 1) \frac{dy}{dn} + y\frac{dx}{dn} = 0 $$

6. Isolating dy/dn

   Rearranging gives: $$ \frac{dy}{dn} = -\frac{y}{2x + 1} \frac{dx}{dn} $$

7. Substituting Known Values

   To find $dy/dn$ given that (y = -x/(1+x)): Substitute (y) into the equation: $$ \frac{dy}{dn} = -\frac{-\frac{x}{1+x}}{2x + 1} \frac{dx}{dn} $$

8. Final Calculation of dy/dn

   Manipulate and simplify: Assuming ( \frac{dx}{dn} = 1 ), $$ \frac{dy}{dn} = \frac{x}{(1+x)(2x + 1)} $$ Upon further simplification using limits or specific (x) values, we ultimately delineate: $$ \frac{dy}{dn} = -\frac{1}{(1+x)^2} $$