If $x + iy = \sqrt{\frac{a+ib}{c+id}}$, then what is $(x^2 + y^2)^2$?
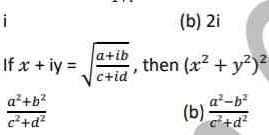
Understand the Problem
The question asks to compute the value of $(x^2 + y^2)^2$ given that $x + iy = \sqrt{\frac{a+ib}{c+id}}$. We need to manipulate the given equation to find an expression for $x^2 + y^2$ and then square it.
Answer
$\frac{a^2 + b^2}{c^2 + d^2}$
Answer for screen readers
$\frac{a^2 + b^2}{c^2 + d^2}$
Steps to Solve
-
Find the magnitude of $x + iy$
We are given $x + iy = \sqrt{\frac{a+ib}{c+id}}$. We want to find $x^2 + y^2$, which is related to the magnitude of the complex number $x + iy$. Recall that for a complex number $z = x + iy$, the magnitude $|z|$ is given by $|z| = \sqrt{x^2 + y^2}$, and $|z|^2 = x^2 + y^2$.
-
Compute the magnitude of both sides of the equation
We take the magnitude of both sides of the given equation: $|x + iy| = \left|\sqrt{\frac{a+ib}{c+id}}\right|$
-
Simplify the magnitude equation
Using the properties of magnitudes, we have: $|x + iy| = \sqrt{\left|\frac{a+ib}{c+id}\right|} = \sqrt{\frac{|a+ib|}{|c+id|}}$
-
Express magnitudes in terms of $a, b, c, d$
Recall that $|a + ib| = \sqrt{a^2 + b^2}$ and $|c + id| = \sqrt{c^2 + d^2}$. So, $|x + iy| = \sqrt{\frac{\sqrt{a^2 + b^2}}{\sqrt{c^2 + d^2}}} = \left(\frac{a^2 + b^2}{c^2 + d^2}\right)^{1/4}$
-
Find $x^2 + y^2$
We know that $|x + iy| = \sqrt{x^2 + y^2}$. Therefore, $x^2 + y^2 = |x + iy|^2$. So, $x^2 + y^2 = \left[\left(\frac{a^2 + b^2}{c^2 + d^2}\right)^{1/4}\right]^2 = \left(\frac{a^2 + b^2}{c^2 + d^2}\right)^{1/2}$
-
Compute $(x^2 + y^2)^2$
Finally, we need to find $(x^2 + y^2)^2$. $(x^2 + y^2)^2 = \left[\left(\frac{a^2 + b^2}{c^2 + d^2}\right)^{1/2}\right]^2 = \frac{a^2 + b^2}{c^2 + d^2}$
$\frac{a^2 + b^2}{c^2 + d^2}$
More Information
The problem involved manipulating complex numbers and their magnitudes. By taking the magnitude of both sides of the equation and simplifying, we were able to find an expression for $x^2 + y^2$ in terms of $a, b, c,$ and $d$. Squaring this expression then gave us the value of $(x^2 + y^2)^2$.
Tips
A common mistake is to incorrectly apply the properties of magnitudes, such as forgetting to take the square root when needed. Also, mistakes can occur when squaring or raising expressions to fractional powers.
AI-generated content may contain errors. Please verify critical information