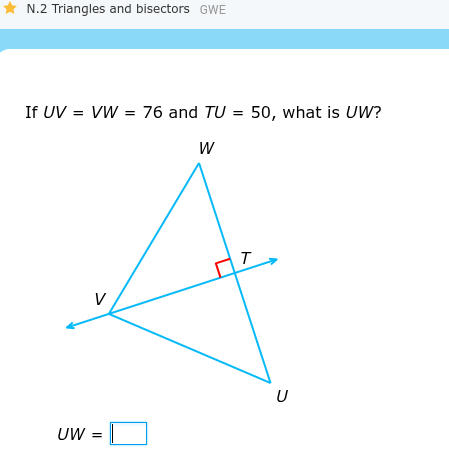
If UV = VW = 76 and TU = 50, what is UW?
Understand the Problem
The question is asking to find the length of side UW of a triangle, given UV = VW = 76 and TU = 50, with the segment VT bisecting angle WVU and being perpendicular to WU. We can solve this using the Pythagorean theorem to find WT and then using the properties of an isosceles triangle and altitude to deduce that WT = TU, and finally solve for UW.
Answer
$UW = 100$
Answer for screen readers
$UW = 100$
Steps to Solve
-
Recognize the Isosceles Triangle Since $UV = VW = 76$, triangle $UVW$ is an isosceles triangle with $V$ as the vertex angle. $VT$ bisects $\angle WVU$, which means $\angle WVT = \angle UVT$. Therefore VT is the altitude and median of the triangle.
-
Recognize $VT$ is Altitude $VT$ is perpendicular to $WU$, therefore $\angle WTU = 90^\circ$.
-
Determine $WT = TU$ Since $VT$ bisects $\angle WVU$ and is perpendicular to $WU$, $VT$ is also a median, which means $WT = TU$. Because $TU = 50$, then $WT = 50$ as well.
-
Calculate $UW$ Since $WT = TU$ and $UW = WT + TU$, we have $UW = 50 + 50 = 100$.
$UW = 100$
More Information
In an isosceles triangle, the angle bisector from the vertex angle to the base is also the altitude and the median to the base. Therefore, the angle bisector divides the base into two equal parts.
Tips
A common mistake could be assuming that $UT = VW$ or $UT = UV$. However, the problem provides enough information to deduce that $UT = WT$. Another mistake might be incorrectly applying the Pythagorean theorem, but this is avoided as the problem doesn't require it.
AI-generated content may contain errors. Please verify critical information