If the function f(x) = { 3ax + b, if x > 1; 11, if x = 1; 5ax - 2b, if x < 1 } is continuous at x = 1, find 'a' and 'b'.
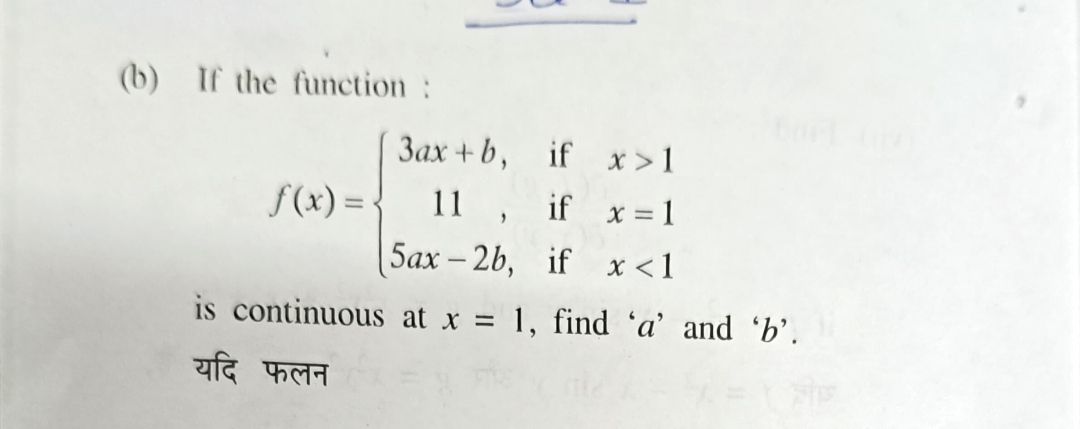
Understand the Problem
The question is asking us to determine the values of 'a' and 'b' such that the given piecewise function is continuous at x = 1. To find continuity at that point, we need to ensure that the limit from the left side and the right side as x approaches 1 are equal to the function's value at x = 1.
Answer
$a = 3$, $b = 2$
Answer for screen readers
The values are ( a = 3 ) and ( b = 2 ).
Steps to Solve
- Identify continuity condition For the function to be continuous at $x = 1$, the left-hand limit, right-hand limit, and the function value at that point must all be equal:
$$ \lim_{x \to 1^-} f(x) = f(1) = \lim_{x \to 1^+} f(x) $$
- Calculate the left-hand limit We find the limit of ( f(x) ) as ( x ) approaches 1 from the left:
$$ \lim_{x \to 1^-} f(x) = 5a(1) - 2b = 5a - 2b $$
- Calculate the function value at x = 1 The function value at ( x = 1 ) is:
$$ f(1) = 11 $$
- Calculate the right-hand limit We find the limit of ( f(x) ) as ( x ) approaches 1 from the right:
$$ \lim_{x \to 1^+} f(x) = 3a(1) + b = 3a + b $$
-
Set up the equations for continuity We set the left-hand limit equal to the function value and the right-hand limit equal to the function value:
-
( 5a - 2b = 11 ) (left limit = function value)
-
( 3a + b = 11 ) (right limit = function value)
-
Solve the system of equations Now we have a system of equations:
-
( 5a - 2b = 11 )
-
( 3a + b = 11 )
To solve, we can express ( b ) from the second equation:
$$ b = 11 - 3a $$
Substitute ( b ) into the first equation:
$$ 5a - 2(11 - 3a) = 11 $$
Simplify and solve for ( a ):
$$ 5a - 22 + 6a = 11 $$
Combine terms:
$$ 11a - 22 = 11 $$
Add 22 to both sides:
$$ 11a = 33 $$
Divide by 11:
$$ a = 3 $$
- Find value of b Substitute ( a = 3 ) back into the equation for ( b ):
$$ b = 11 - 3(3) $$
This simplifies to:
$$ b = 11 - 9 = 2 $$
The values are ( a = 3 ) and ( b = 2 ).
More Information
The solution ensures that the piecewise function is continuous at ( x = 1 ). This process involves determining the limits and the function's value at that point, ensuring all are equal, which is a key property of continuous functions.
Tips
- Forgetting to equate the left-hand and right-hand limits to the function value, which is crucial for establishing continuity.
- Miscalculating when substituting values into equations, especially while solving for ( a ) and ( b ). It can help to double-check calculations after solving.
