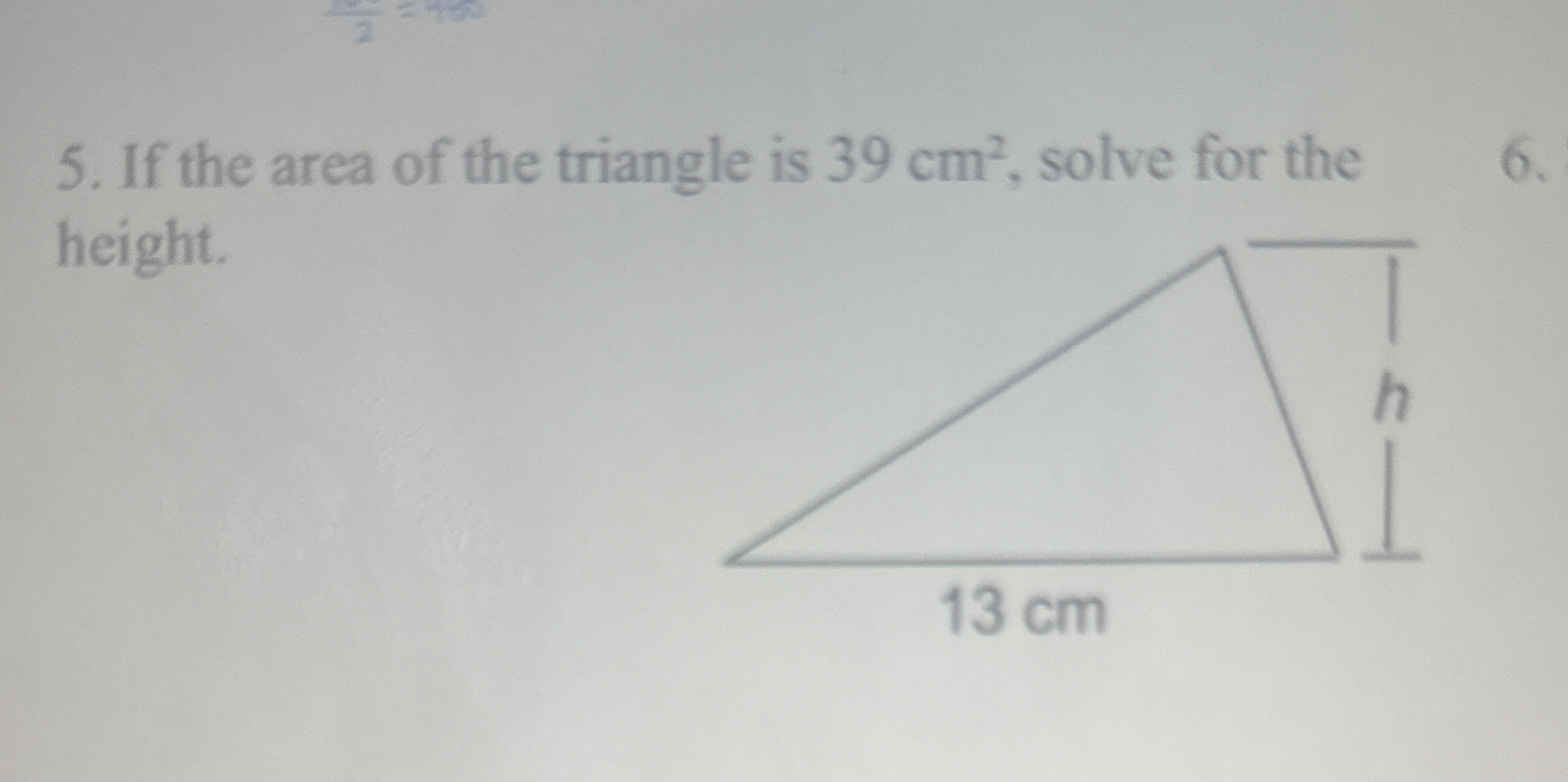
If the area of the triangle is 39 cm², solve for the height.
Understand the Problem
The question is asking to solve for the height of a triangle given its area and the base length. The area of a triangle is calculated using the formula: Area = (1/2) * base * height. Here, the area is 39 cm² and the base is 13 cm, so we need to rearrange the formula to find the height (h).
Answer
The height of the triangle is $h = 6 \, \text{cm}$.
Answer for screen readers
The height of the triangle is $h = 6 , \text{cm}$.
Steps to Solve
- Write the Area Formula The formula for the area of a triangle is given by:
$$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} $$
- Substitute Known Values Substituting the given values for area and base into the formula. The area is 39 cm², and the base is 13 cm:
$$ 39 = \frac{1}{2} \times 13 \times h $$
- Clear the Fraction Multiply both sides of the equation by 2 to eliminate the fraction:
$$ 2 \times 39 = 13 \times h $$
This simplifies to:
$$ 78 = 13h $$
- Solve for Height Now, divide both sides by 13 to solve for height $h$:
$$ h = \frac{78}{13} $$
- Calculate the Height Compute the value of $h$:
$$ h = 6 , \text{cm} $$
The height of the triangle is $h = 6 , \text{cm}$.
More Information
The area formula for a triangle shows how the height and base work together to determine the area. In this case, knowing either base or height allows us to find the other.
Tips
- Forgetting to multiply both sides of the equation by 2 before dividing can lead to an incorrect value for height.
- Miscalculating the division when finding height from the equation can also result in errors.
AI-generated content may contain errors. Please verify critical information