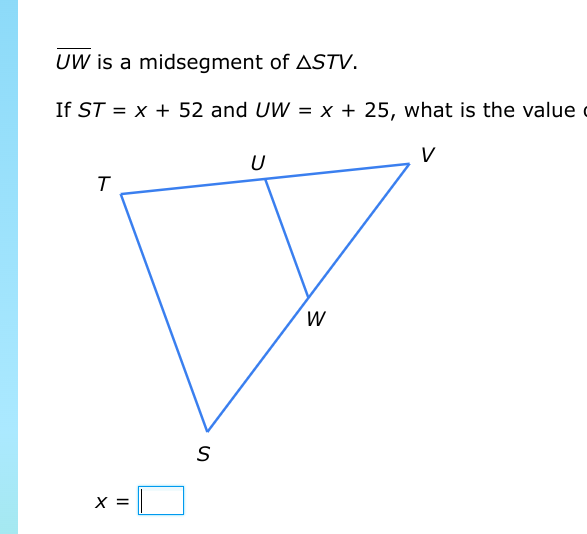
If ST = x + 52 and UW = x + 25, what is the value of x?
Understand the Problem
The question is asking us to find the value of x based on the information provided about segments in triangle STV. Specifically, we need to set up an equation using the properties of the midsegment.
Answer
\(x = 2\)
Answer for screen readers
The value of (x) is (2).
Steps to Solve
-
Understand the Midsegment Property The midsegment of a triangle is parallel to the third side and its length is half the length of that side. In this case, since (UW) is the midsegment, we have: $$ UW = \frac{1}{2} ST $$
-
Set Up the Equation Using the midsegment property, substitute the expressions for (ST) and (UW): $$ x + 25 = \frac{1}{2} (x + 52) $$
-
Eliminate the Fraction Multiply both sides by 2 to eliminate the fraction: $$ 2(x + 25) = x + 52 $$
-
Distribute Distribute on the left side: $$ 2x + 50 = x + 52 $$
-
Isolate (x) Subtract (x) from both sides to isolate (x): $$ 2x - x + 50 = 52 $$
-
Simplify This simplifies to: $$ x + 50 = 52 $$
-
Solve for (x) Finally, subtract 50 from both sides: $$ x = 52 - 50 $$ $$ x = 2 $$
The value of (x) is (2).
More Information
This example illustrates how the properties of triangles, specifically the midsegment, are used to create relationships between the lengths of sides. In this case, we found (x) by setting up an equation based on the midsegment property.
Tips
- Forgetting to use the midsegment property, which leads to incorrect equations.
- Miscalculating during distribution or simplification, making arithmetic errors.
AI-generated content may contain errors. Please verify critical information