If sin(A) = 3/5 and cos(B) = 15/17 where A and B are acute angles, find the exact value of sin(A+B).
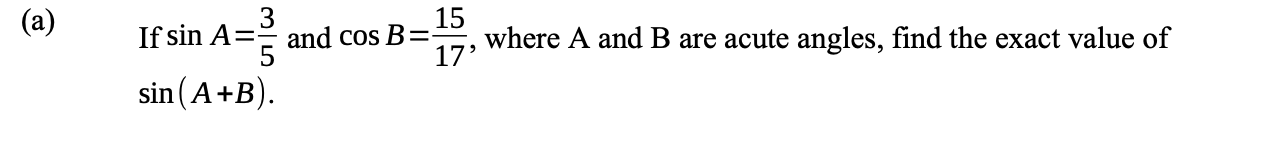
Understand the Problem
The question asks to find the exact value of sin(A+B) given that sin(A) = 3/5 and cos(B) = 15/17, where A and B are acute angles. We can use the sine addition formula sin(A+B) = sin(A)cos(B) + cos(A)sin(B) to solve this problem. First, determine the values of cos(A) and sin(B) using the Pythagorean identity.
Answer
$\frac{77}{85}$
Answer for screen readers
$\frac{77}{85}$
Steps to Solve
- Find $\cos A$ using the Pythagorean identity
Since $\sin^2 A + \cos^2 A = 1$, we have $\cos^2 A = 1 - \sin^2 A$. Substituting $\sin A = \frac{3}{5}$, we get $$ \cos^2 A = 1 - \left(\frac{3}{5}\right)^2 = 1 - \frac{9}{25} = \frac{16}{25} $$ Since A is an acute angle, $\cos A$ is positive. Therefore, $\cos A = \sqrt{\frac{16}{25}} = \frac{4}{5}$.
- Find $\sin B$ using the Pythagorean identity
Since $\sin^2 B + \cos^2 B = 1$, we have $\sin^2 B = 1 - \cos^2 B$. Substituting $\cos B = \frac{15}{17}$, we get $$ \sin^2 B = 1 - \left(\frac{15}{17}\right)^2 = 1 - \frac{225}{289} = \frac{64}{289} $$ Since B is an acute angle, $\sin B$ is positive. Therefore, $\sin B = \sqrt{\frac{64}{289}} = \frac{8}{17}$.
- Use the sine addition formula
The sine addition formula is $\sin(A+B) = \sin A \cos B + \cos A \sin B$. Substituting the known values, we have $$ \sin(A+B) = \left(\frac{3}{5}\right)\left(\frac{15}{17}\right) + \left(\frac{4}{5}\right)\left(\frac{8}{17}\right) $$
- Calculate $\sin(A+B)$
$$ \sin(A+B) = \frac{45}{85} + \frac{32}{85} = \frac{45+32}{85} = \frac{77}{85} $$
$\frac{77}{85}$
More Information
The final answer is $\frac{77}{85}$. This is the exact value of $\sin(A+B)$, given the information in the problem statement.
Tips
A common mistake is forgetting to consider the sign of $\cos A$ and $\sin B$. Since A and B are acute angles, both $\cos A$ and $\sin B$ are positive. Another common mistake is making an arithmetic error when calculating $\sin(A+B)$.
AI-generated content may contain errors. Please verify critical information