If sigma1 is the surface charge on the inner surface and sigma2 the surface charge on the outer surface of the shell, what is the relation between Q1, Q2, sigma1, and sigma2 if Q1... If sigma1 is the surface charge on the inner surface and sigma2 the surface charge on the outer surface of the shell, what is the relation between Q1, Q2, sigma1, and sigma2 if Q1 is the charge at the center of the cavity?
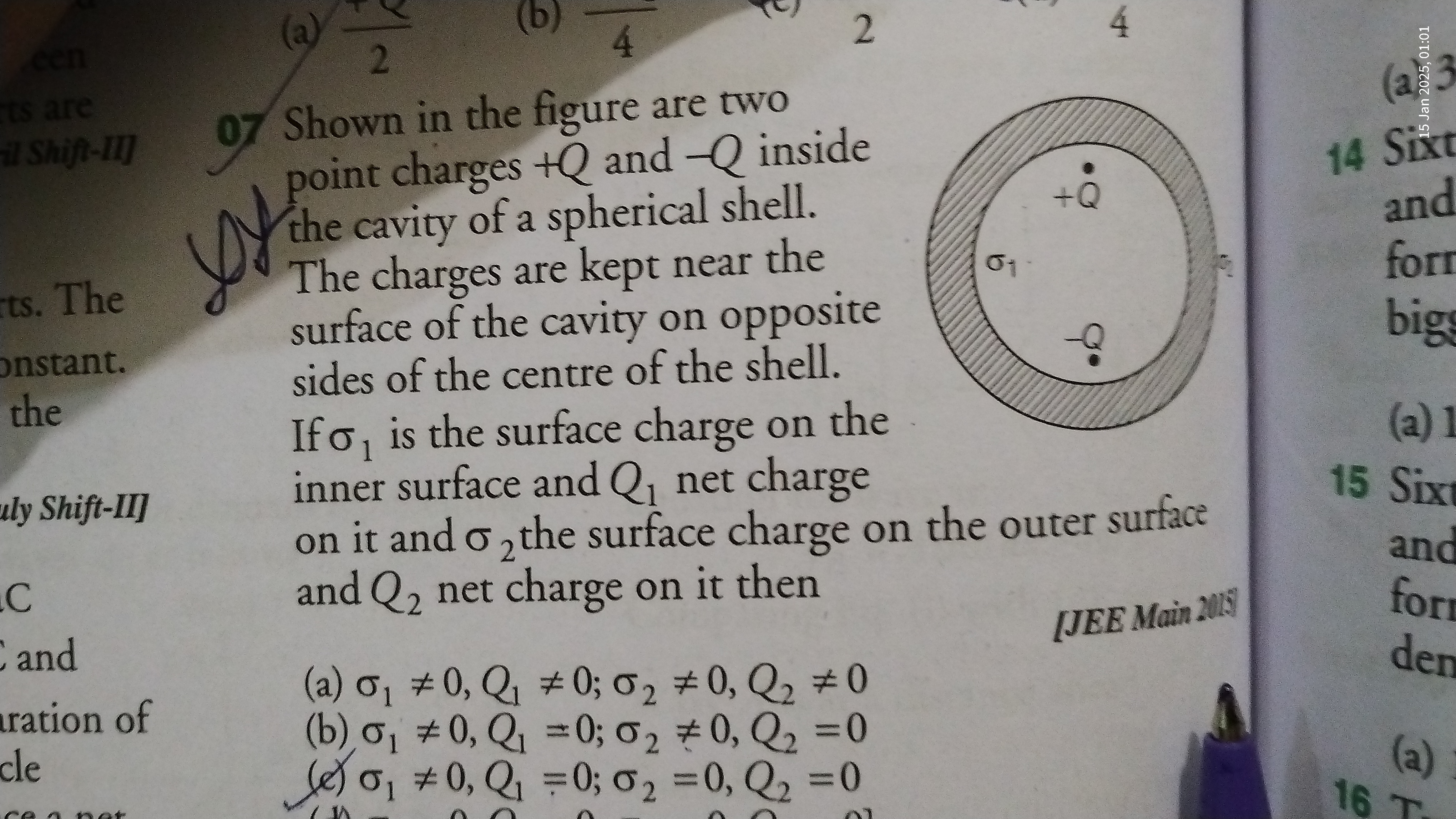
Understand the Problem
The question is asking about the charge distribution on the surfaces of a spherical shell that contains two point charges inside it. We need to analyze how the charges on the inner and outer surfaces of the shell are affected by the presence of these point charges and to determine the net charge on those surfaces.
Answer
The relations are $σ_1 = -\frac{Q_1}{A_1}$ and $σ_2 = \frac{Q_1 + Q_2}{A_2}$.
Answer for screen readers
The relation between the charges and surface charge densities is given by: $$ σ_1 = -\frac{Q_1}{A_1} \quad \text{and} \quad σ_2 = \frac{Q_1 + Q_2}{A_2} $$
Steps to Solve
-
Understanding charge distribution inside the shell When a point charge $Q_1$ is placed inside the cavity of the spherical shell, it induces a surface charge $σ_1$ on the inner surface of the shell. The total induced charge on the inner surface must balance the electric field produced by the charge inside.
-
Calculating the induced inner surface charge The induced surface charge $σ_1$ on the inner surface is equal to the negative of the enclosed charge. If $Q_1$ has a charge of $+q$, then: $$ σ_1 = -\frac{Q_1}{A_1} $$ where $A_1$ is the area of the inner surface.
-
Understanding charge distribution on the outer surface The spherical shell is neutral overall. Therefore, the total charge on the outer surface $σ_2$ must balance the charge induced on the inner surface. Hence: $$ Q_{total} = 0 \Rightarrow Q_{outer} = -Q_{inner} $$
-
Calculating the outer surface charge If $Q_2$ is the other point charge placed inside, the induced charge on the outer surface can be expressed as: $$ σ_2 = \frac{Q_1 + Q_2}{A_2} $$ where $A_2$ is the area of the outer surface.
-
Relating the charges From the above steps, we conclude:
- The inner surface charge is $\sigma_1 = -Q_1/A_1$.
- The outer surface charge is $\sigma_2 = \frac{Q_1 + Q_2}{A_2}$.
The relation between the charges and surface charge densities is given by: $$ σ_1 = -\frac{Q_1}{A_1} \quad \text{and} \quad σ_2 = \frac{Q_1 + Q_2}{A_2} $$
More Information
The spherical shell's behavior with regards to charge distribution is a fundamental concept in electrostatics, illustrating how electric fields interact within conductive materials. This principle is crucial in capacitors and other electrical applications.
Tips
- Ignoring overall neutrality: Students often forget that the spherical shell must remain electrically neutral overall.
- Assuming uniform charge distribution: The charge may not be uniformly distributed, especially when different charges are involved inside the shell.
AI-generated content may contain errors. Please verify critical information