If P(A) = 0.8, P(B) = 0.5 and P(B|A) = 0.4. Find P(A ∩ B).
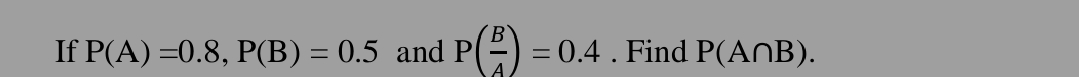
Understand the Problem
The question is asking to find the probability of the intersection of two events A and B given several probabilities. This involves applying the rules of probability, specifically relating conditional probabilities and using the provided values.
Answer
The probability \( P(A \cap B) = 0.32 \).
Answer for screen readers
The probability ( P(A \cap B) = 0.32 ).
Steps to Solve
- Understand the Formula for Intersection of Events
To find the probability of the intersection of two events, we can use the formula:
$$ P(A \cap B) = P(B|A) \cdot P(A) $$
This means we multiply the conditional probability of B given A by the probability of A.
- Plug in the Known Values
From the problem, we have:
- ( P(A) = 0.8 )
- ( P(B|A) = 0.4 )
Substituting these values into the formula:
$$ P(A \cap B) = P(B|A) \cdot P(A) = 0.4 \cdot 0.8 $$
- Calculate the Final Probability
Now we compute the product:
$$ P(A \cap B) = 0.4 \cdot 0.8 = 0.32 $$
The probability ( P(A \cap B) = 0.32 ).
More Information
This result tells us that there is a 32% chance that both events A and B occur simultaneously. Understanding conditional probability is key in various fields, including statistics and risk assessment.
Tips
- Confusing conditional probability with unconditional probability. Make sure to use the proper formula.
- Forgetting to multiply the probabilities correctly. Always double-check your calculations.
AI-generated content may contain errors. Please verify critical information