If ω = 2π/T = 2πf then:
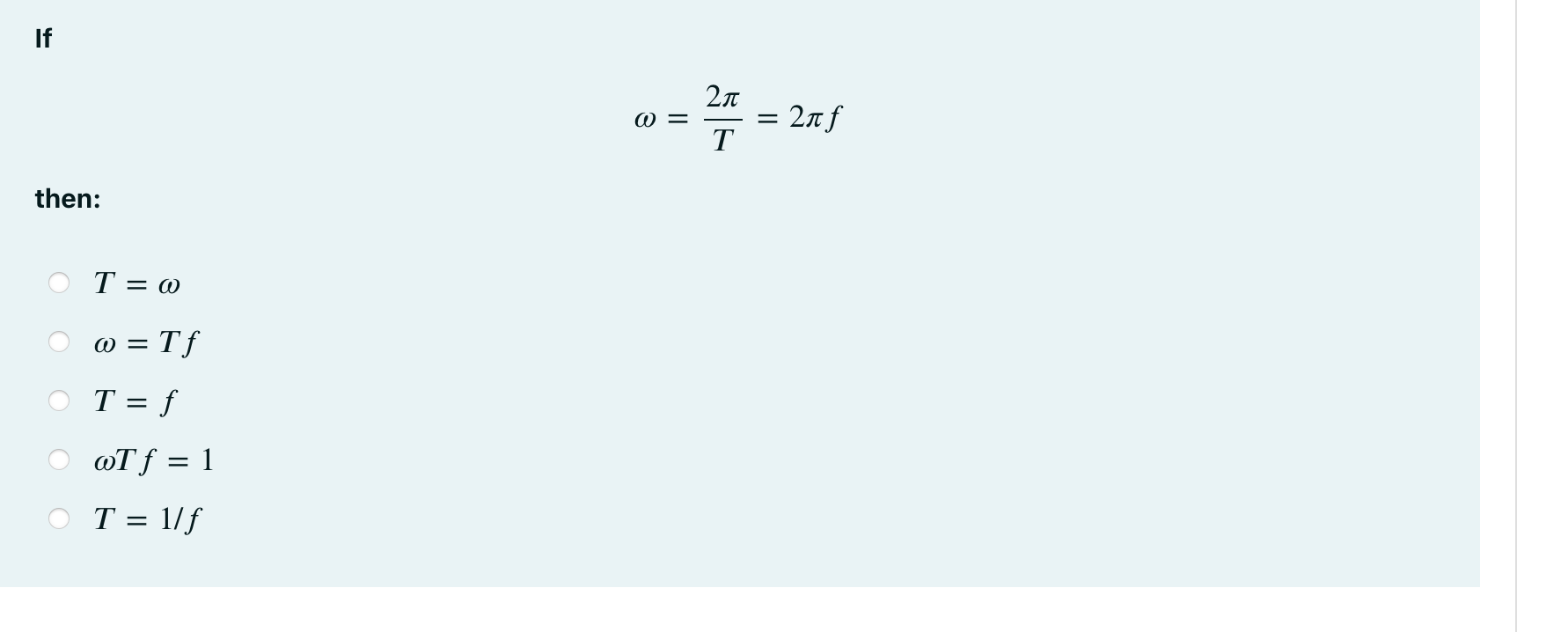
Understand the Problem
The question provides a mathematical equation related to angular frequency (ω) and is asking to determine the correct relationship among the options given. It tests the knowledge of fundamental physics concepts related to oscillatory motion.
Answer
$T = \frac{1}{f}$, $\omega = Tf$
Answer for screen readers
The correct relationships are ( T = \frac{1}{f} ) and ( \omega = T f ).
Steps to Solve
-
Understanding Relationships We have the equation for angular frequency given by ( \omega = \frac{2\pi}{T} = 2\pi f ). This implies that angular frequency ( \omega ) is inversely proportional to the time period ( T ) and directly proportional to the frequency ( f ).
-
Rearranging the First Equation Starting from the equation ( \omega = \frac{2\pi}{T} ), we can rearrange it to solve for ( T ): $$ T = \frac{2\pi}{\omega} $$
-
Relating Frequency and Period From the equation ( \omega = 2\pi f ), we can express the frequency ( f ) in terms of angular frequency ( \omega ): $$ f = \frac{\omega}{2\pi} $$
-
Finding the Period in Relation to Frequency Using the relationship between frequency and period, where ( T = \frac{1}{f} ), we substitute ( f ): $$ T = \frac{1}{\frac{\omega}{2\pi}} = \frac{2\pi}{\omega} $$
-
Identifying Correct Options From the rearrangements:
- We see ( T \neq \omega ) and ( T \neq f ).
- The relation ( \omega = T f ) can be derived since ( \omega = 2\pi f ).
- Hence, the options ( \omega T f = 1 ) does not hold true and ( T = 1/f ) is valid.
The correct relationships are ( T = \frac{1}{f} ) and ( \omega = T f ).
More Information
The fundamental relationships of angular frequency, frequency, and period illustrate how they interconnect in oscillatory motion. Understanding these can help in analyzing various physical systems like springs and pendulums.
Tips
- Mixing up the relationships between ( T ), ( f ), and ( \omega ) can lead to confusion.
- Always remember that ( T ) and ( f ) are inversely related, and double-check equations for proper arrangement before deriving conclusions.
AI-generated content may contain errors. Please verify critical information