If n(U) = 40, n(A') = 12, n(B') = 18 and n(A ∩ B) = 20 then n(A ∪ B), where U is the universal set, is?
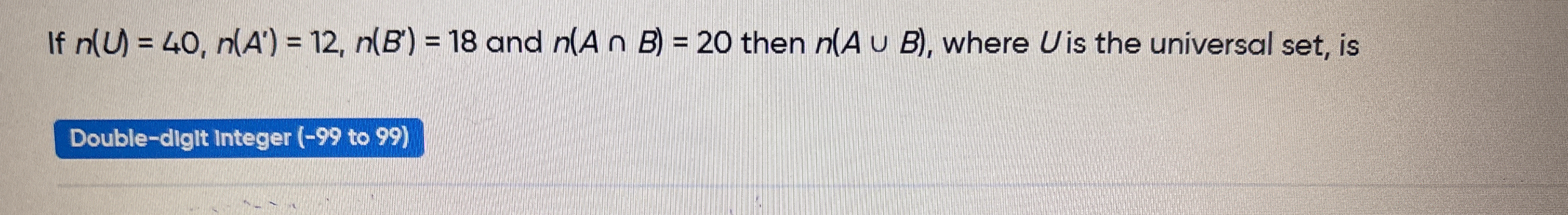
Understand the Problem
The question is asking for the number of elements in the union of two sets A and B, given the total elements in the universal set and the size of sets A and B along with their intersections. We will use the formula for the union of two sets: n(A ∪ B) = n(A) + n(B) - n(A ∩ B).
Answer
The number of elements in \( A \cup B \) is \( 10 \).
Answer for screen readers
The number of elements in ( A \cup B ) is ( n(A \cup B) = 10 ).
Steps to Solve
- Identify given values We have the following information:
- Total elements in the universal set: ( n(U) = 40 )
- Size of set ( A ): ( n(A) = 12 )
- Size of set ( B ): ( n(B) = 18 )
- Size of the intersection of sets ( A ) and ( B ): ( n(A \cap B) = 20 )
-
Apply the formula for the union of sets To find the number of elements in the union of sets ( A ) and ( B ), we need to use the formula: $$ n(A \cup B) = n(A) + n(B) - n(A \cap B) $$
-
Plug in the values Now substitute the known values into the formula: $$ n(A \cup B) = 12 + 18 - 20 $$
-
Calculate the union Calculate the result from the substitution: $$ n(A \cup B) = 30 - 20 = 10 $$
The number of elements in ( A \cup B ) is ( n(A \cup B) = 10 ).
More Information
The union of two sets represents all the elements that are in either set. In this case, the result indicates that there are 10 unique elements in either set ( A ) or ( B ). Since the size of the intersection is higher than the individual sizes of both sets, it suggests that most elements are shared between ( A ) and ( B ).
Tips
- Forgetting to subtract the intersection, which leads to overcounting elements that are in both sets.
- Misidentifying total elements or intersection sizes can skew the results.
AI-generated content may contain errors. Please verify critical information