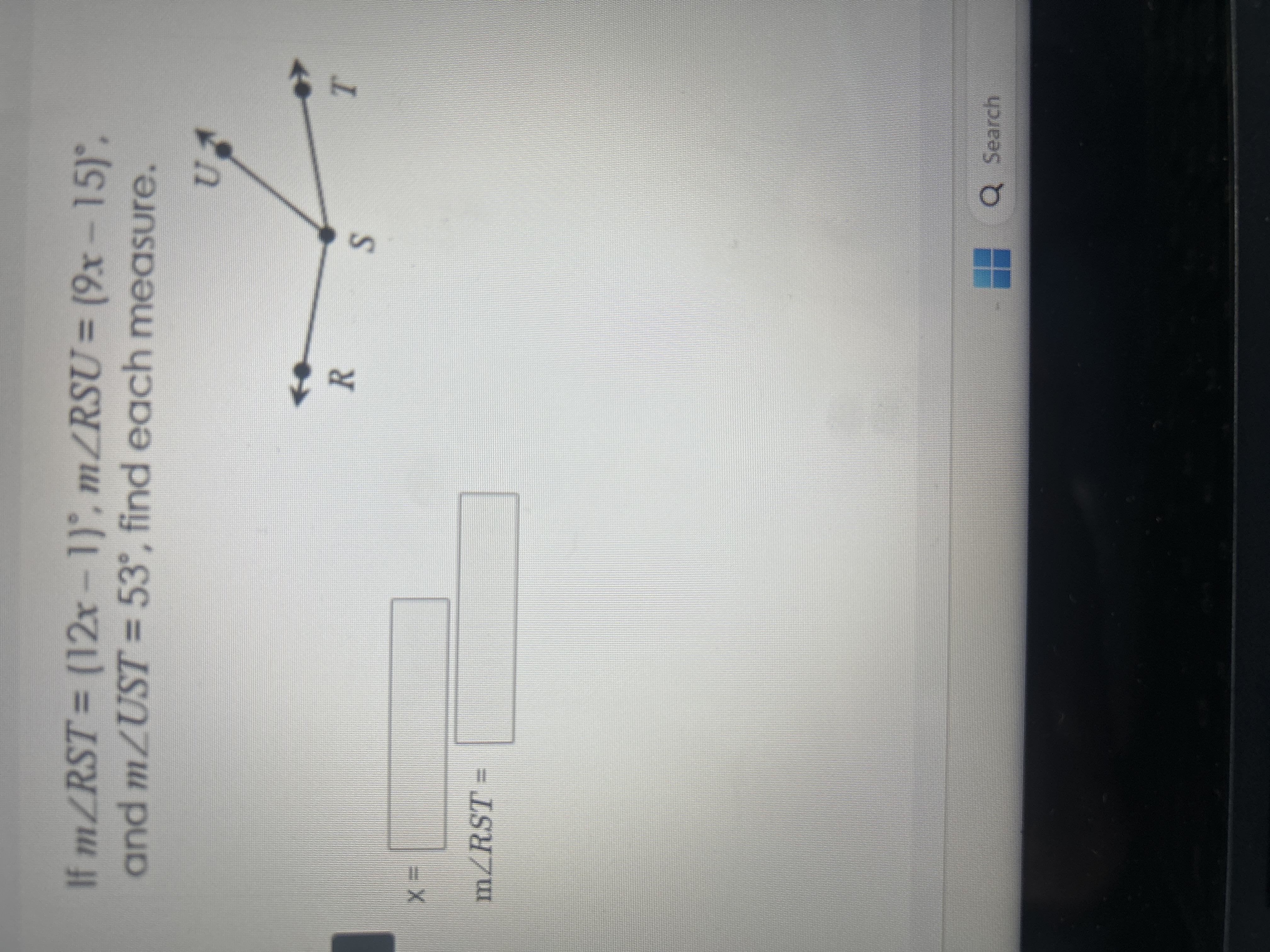
If m∠RST = (12x - 1)°, m∠RSU = (9x - 15)°, and m∠UST = 53°, find each measure.

Understand the Problem

The question is asking to find the value of x and the measure of angle RST using the given angle expressions and the relationship between the angles around point S. This involves setting up equations based on the provided angle measures and solving for the unknowns.

Answer

$x \approx 6.81$, $m\angle RST \approx 80.67^\circ$

Steps to Solve

Identify angle relationships at point S We know that the sum of the angles around point S should equal $180^\circ$, as angles RST, RSU, and UST are all supplementary. So, we have the equation: $$ m\angle RST + m\angle RSU + m\angle UST = 180^\circ $$
Substituting the given angle expressions Now substitute the expressions into the equation: $$ (12x - 1) + (9x - 15) + 53 = 180 $$
Combine like terms Combine the terms in the equation: $$ 12x + 9x - 1 - 15 + 53 = 180 $$ This simplifies to: $$ 21x + 37 = 180 $$
Solve for x Now isolate x by subtracting 37 from both sides: $$ 21x = 180 - 37 $$ $$ 21x = 143 $$ Now, divide by 21: $$ x = \frac{143}{21} $$ This further simplifies to: $$ x \approx 6.81 $$
Calculate the measure of angle RST Now, substitute the value of x back into the expression for angle RST: $$ m\angle RST = 12x - 1 $$ $$ m\angle RST = 12\left(\frac{143}{21}\right) - 1 $$ $$ m\angle RST \approx 80.67^\circ $$

The value of $x$ is approximately $6.81$ and the measure of angle $RST$ is approximately $80.67^\circ$.

More Information

This problem involves an understanding of angle relationships and algebraic manipulation. The angles around a point sum to $180^\circ$, which is a critical concept in geometry.

Tips

Confusing supplementary angles with complementary angles; remember that supplementary angles sum to $180^\circ$.
Not combining like terms correctly; double-check your arithmetic when simplifying equations.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!