If m = a^{1/3} + a^{-1/3}, prove that: m^3 - 3m = a + 1/a.
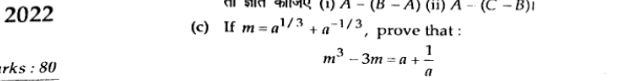
Understand the Problem
The question is asking us to prove a mathematical statement involving the variable m, which is defined in terms of a. The equation to prove is m^3 - 3m = a + 1/a.
Answer
$$ m^3 - 3m = a + \frac{1}{a} $$
Answer for screen readers
$$ m^3 - 3m = a + \frac{1}{a} $$
Steps to Solve
- Express ( m ) in terms of ( a )
Given that ( m = a^{1/3} + a^{-1/3} ), we can denote: $$ x = a^{1/3} $$ Thus, $$ m = x + \frac{1}{x} $$
- Calculate ( m^3 )
Using the expression for ( m ): $$ m^3 = \left( x + \frac{1}{x} \right)^3 $$
Expanding the cube: $$ m^3 = x^3 + 3x^2\left(\frac{1}{x}\right) + 3x\left(\frac{1}{x^2}\right) + \frac{1}{x^3} $$ This simplifies to: $$ m^3 = x^3 + 3\left(x + \frac{1}{x}\right) + \frac{1}{x^3} $$
Recognizing that ( x^3 = a ) and ( \frac{1}{x^3} = \frac{1}{a} ), we have: $$ m^3 = a + 3m + \frac{1}{a} $$
- Rearranging the equation
Now, rewrite the equation: $$ m^3 - 3m = a + \frac{1}{a} $$
- Final Statement
This shows that: $$ m^3 - 3m = a + \frac{1}{a} $$ This is exactly what we wanted to prove.
$$ m^3 - 3m = a + \frac{1}{a} $$
More Information
The proof utilizes the identity for the sum of cubes and properties of exponents. The result demonstrates the relationships between ( m ) and ( a ), showing how the cubic expression reduces elegantly through simplification.
Tips
- Mistakenly forgetting to expand the cube correctly.
- Neglecting to apply the relationship of ( x^3 ) and ( \frac{1}{x^3} ) leading to confusion in simplifying the equation.
AI-generated content may contain errors. Please verify critical information