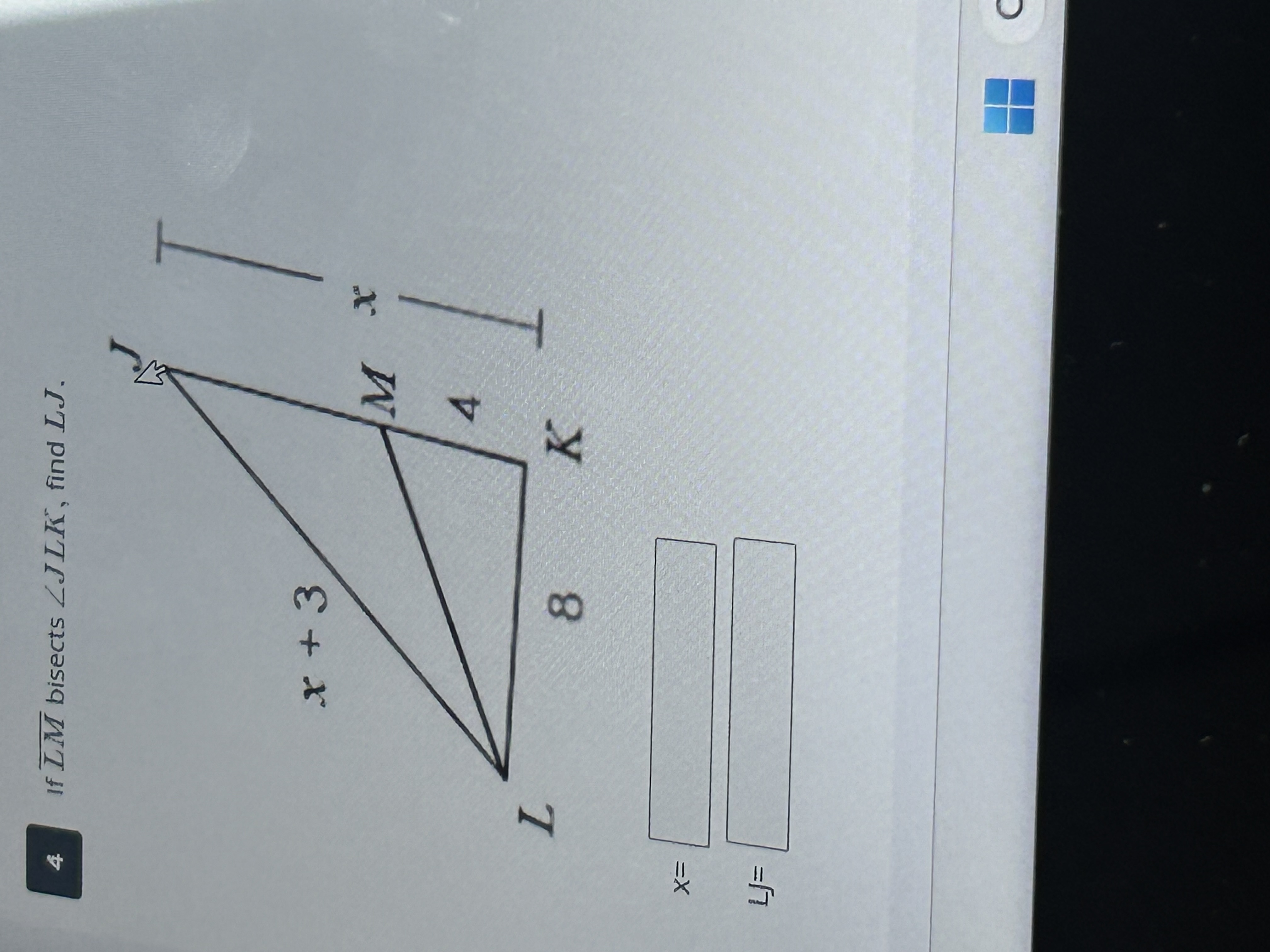
If LM bisects angle JLK, find LJ.
Understand the Problem
The problem presents a triangle JKL where LM bisects angle JLK. We are given the lengths MK = 4, LK = 8 and LJ = x + 3, and need to find the value of x and the length of LJ. Since LM bisects (\angle JLK), we can use the Angle Bisector Theorem, which states that the ratio of LJ to LK is equal to the ratio of JM to MK. In other words, we can set up the proportion (\frac{LJ}{LK} = \frac{JM}{MK}), then solve for x, and then find LJ.
Answer
x = 3 LJ = 6
Answer for screen readers
x = 3 LJ = 6
Steps to Solve
-
Apply the Angle Bisector Theorem Since $LM$ bisects $\angle JLK$, we have $\frac{LJ}{LK} = \frac{JM}{MK}$. We know that $LJ = x + 3$, $LK = 8$, $MK = 4$ and $JM = x$ So we have the proportion $\frac{x+3}{8} = \frac{x}{4}$.
-
Solve for x Cross multiply to get rid of the fractions: $$4(x+3) = 8x$$ Expand the left side: $$4x + 12 = 8x$$ Subtract $4x$ from both sides: $$12 = 4x$$ Divide both sides by 4: $$x = \frac{12}{4} = 3$$
-
Find LJ Since $LJ = x + 3$, substitute $x = 3$: $$LJ = 3 + 3 = 6$$
x = 3 LJ = 6
More Information
The Angle Bisector Theorem is a powerful tool for solving problems involving triangles and angle bisectors, establishing a direct relationship between the sides of the triangle and the segments created by the angle bisector.
Tips
A common mistake is to incorrectly set up the proportion. Ensure that the corresponding sides are in the correct ratio. For instance, mixing up LJ with LK or JM with MK would lead to an incorrect equation. Also, mistakes in the algebra to isolate x are common.
AI-generated content may contain errors. Please verify critical information