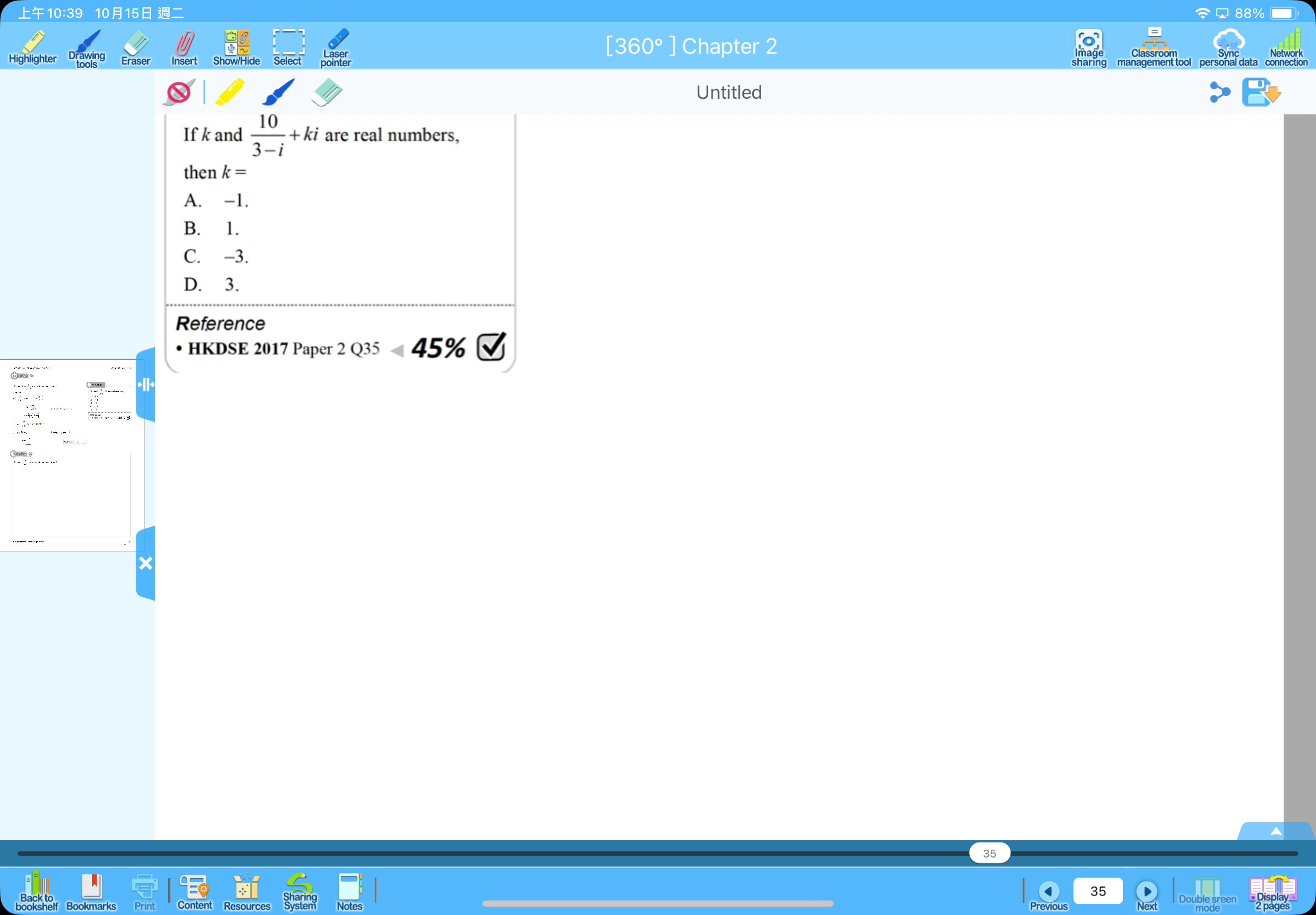
If k and \(\frac{10}{3-i} + ki\) are real numbers, then k = ?
Understand the Problem
The question is asking to find the value of 'k' such that the expression (\frac{10}{3-i} + ki) results in a real number. This involves manipulating complex numbers to eliminate the imaginary part.
Answer
A. -1
Answer for screen readers
A. -1
Steps to Solve
-
Rationalize the complex number To get rid of the imaginary part in the denominator, multiply both the numerator and the denominator of $\frac{10}{3-i}$ by the conjugate of the denominator, which is $3+i$.
-
Multiply by the conjugate $$ \frac{10}{3-i} \cdot \frac{3+i}{3+i} = \frac{10(3+i)}{(3-i)(3+i)} $$
-
Simplify the expression The denominator becomes $3^2 - (i)^2 = 9 - (-1) = 10$. So, $$ \frac{10(3+i)}{10} = 3+i $$
-
Set up the equation We are given that $\frac{10}{3-i} + ki$ is a real number. Substitute the simplified expression: $$ 3 + i + ki $$
-
Factor out $i$ $$ 3 + (1+k)i $$
-
Solve for k For the expression to be a real number, the imaginary part must be equal to zero. That is, $$ 1 + k = 0 $$ Solving for $k$ gives: $$ k = -1 $$
A. -1
More Information
When dealing with complex numbers, multiplying by the conjugate is a common technique to rationalize the denominator and simplify expressions.
Tips
- Forgetting to multiply both the numerator and denominator by the conjugate.
- Incorrectly calculating $(3-i)(3+i)$. A common mistake is to forget that $i^2 = -1$.
AI-generated content may contain errors. Please verify critical information