If g(x + 3) = x^2 + 2, then g(x) equals:
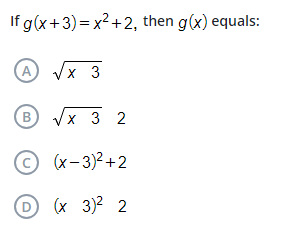
Understand the Problem
The question is asking to find the function g(x) based on the given equation g(x + 3) = x^2 + 2. To solve this, we will need to express g in terms of x by substituting x + 3 and then rearranging the equation to isolate g(x).
Answer
$$ g(x) = (x - 3)^2 + 2 $$
Answer for screen readers
$$ g(x) = (x - 3)^2 + 2 $$
Steps to Solve
-
Substituting the variable To isolate $g(x)$, replace $x$ in the original equation with $(x - 3)$: $$ g(x) = (x - 3)^2 + 2 $$
-
Expressing in terms of x Now we have: $$ g(x) = (x - 3)^2 + 2 $$
-
Final expression This is the function $g(x)$ in terms of $x$.
$$ g(x) = (x - 3)^2 + 2 $$
More Information
The function $g(x)$ describes a parabola that opens upward, with its vertex at the point (3, 2). This transformation shifts the standard parabola $y = x^2$ to the right by 3 units and up by 2 units.
Tips
- Incorrect substitution: Sometimes, learners might incorrectly substitute or misinterpret the transformations. Always ensure to follow the specified change from $x + 3$ to $x$ properly.
AI-generated content may contain errors. Please verify critical information