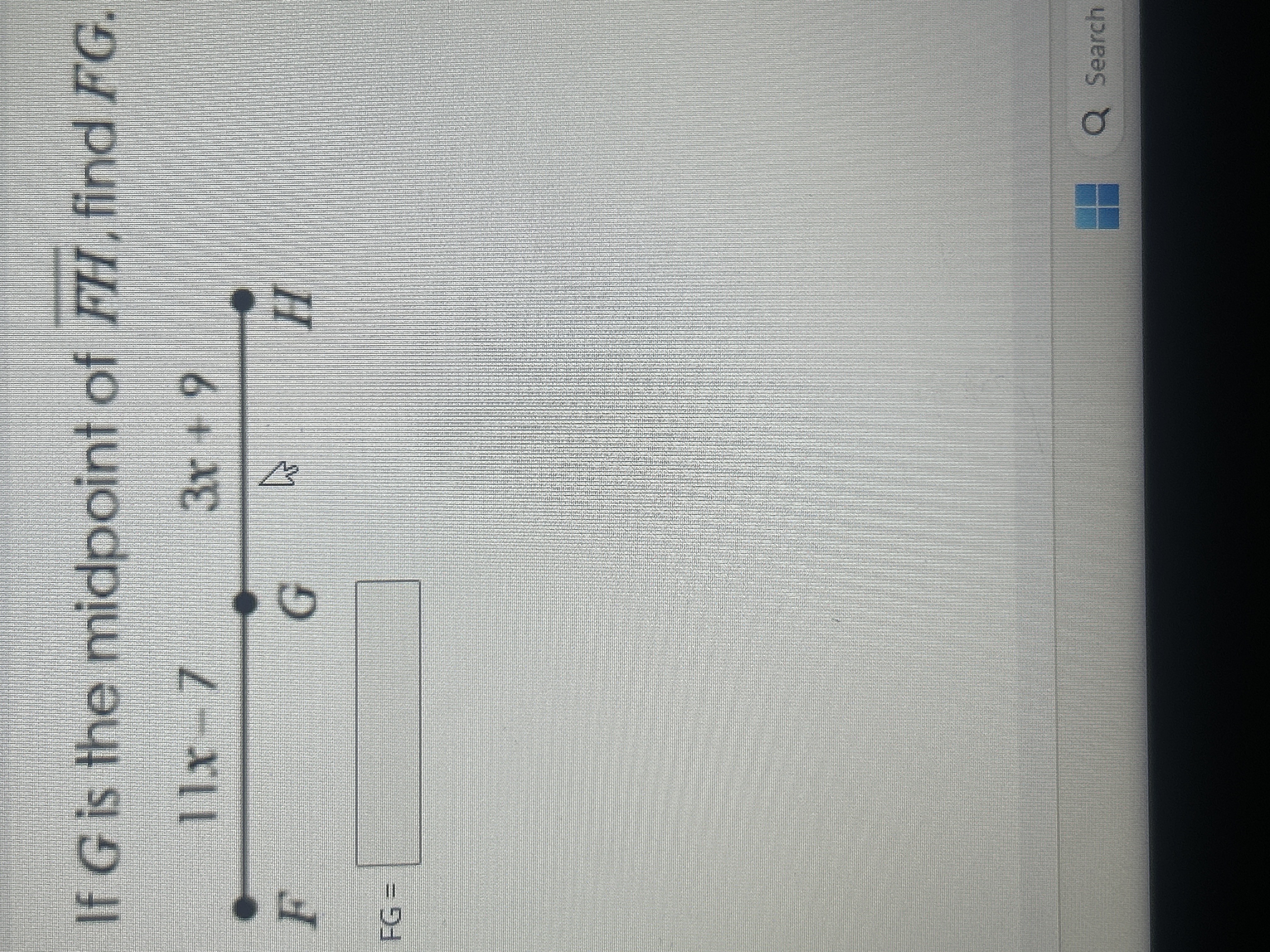
If G is the midpoint of FH, find FG.
Understand the Problem
The question is asking us to find the length of segment FG, given that G is the midpoint of segment FH, and we have expressions for the lengths of FG and GH. We can set up an equation using the property of midpoints.
Answer
FG = $15$
Answer for screen readers
The length of segment FG is $15$.
Steps to Solve
- Understand the Relationship of Segments
Since G is the midpoint of FH, this means that the lengths of segments FG and GH are equal.
- Set Up the Equation
We can express this relationship mathematically: $$ FG = GH $$
Given:
- $ FG = 11x - 7 $
- $ GH = 3x + 9 $
Setting the two expressions equal gives: $$ 11x - 7 = 3x + 9 $$
- Solve for x
First, we will isolate x by subtracting $3x$ from both sides: $$ 11x - 3x - 7 = 9 $$
This simplifies to: $$ 8x - 7 = 9 $$
Next, add 7 to both sides: $$ 8x = 16 $$
Now, divide by 8: $$ x = 2 $$
- Find FG
Now that we have the value of x, substitute it back into the expression for FG: $$ FG = 11(2) - 7 $$
Calculating this gives: $$ FG = 22 - 7 = 15 $$
The length of segment FG is $15$.
More Information
This problem demonstrates how midpoints divide segments into two equal parts and how to solve equations by isolating variables. Knowing that G is the midpoint allows us to set up a simple equation.
Tips
- Not setting the lengths equal: Some might forget that G being the midpoint means FG equals GH.
- Incorrect arithmetic while solving for x: Double-check each step of basic operations to avoid mistakes.
AI-generated content may contain errors. Please verify critical information