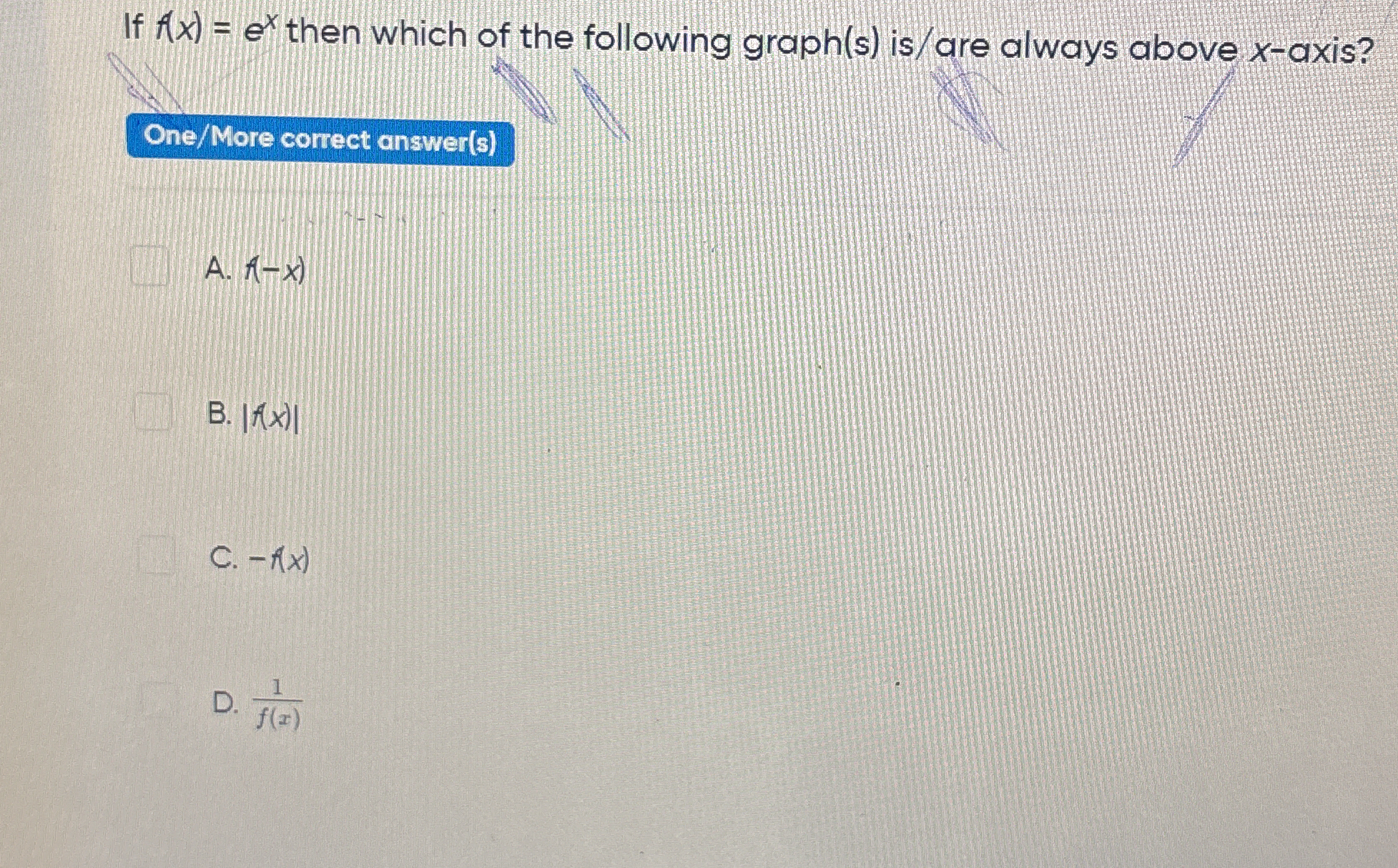
If f(x) = e^x then which of the following graphs(s) is/are always above x-axis?
Understand the Problem
The question is asking which of the provided functions based on f(x) = e^x are always above the x-axis. This implies that we need to analyze each option to determine if the respective transformations of f(x) keep the values positive for all x.
Answer
The functions always above the x-axis are A, B, and D.
Answer for screen readers
The correct answers are A, B, and D.
Steps to Solve
-
Understand the Function f(x)
The function given is $f(x) = e^x$. This function is always positive for all real numbers $x$ since the exponential function does not cross the x-axis.
-
Analyze Each Option
We will evaluate each transformation to see if it remains above the x-axis.
-
Option A: $f(-x)$
This is $e^{-x}$, which is also always positive for all $x$. Thus, $f(-x) > 0$ for all $x$.
-
Option B: $|f(x)|$
This is $|e^x|$. Since $e^x$ is always positive, $|f(x)| = e^x > 0$ for all $x$.
-
Option C: $-f(x)$
This becomes $-e^x$. Since $e^x$ is always positive, $-f(x) < 0$ for all $x$. Therefore, it does not stay above the x-axis.
-
Option D: $\frac{1}{f(x)}$
This is $\frac{1}{e^x}$. As $e^x$ is always positive, $\frac{1}{f(x)} > 0$ for all $x$.
-
-
Summarize Results
From analyzing all options:
- The functions that are always above the x-axis are Options A, B, and D.
The correct answers are A, B, and D.
More Information
The exponential function $f(x) = e^x$ is crucial in calculus and many areas of mathematics because it has unique properties, such as always being positive. The transformations of this function interact in interesting ways with its properties, showing how different manipulations can affect the overall behavior.
Tips
- Confusing transformations that merely reflect or translate the graph (like $f(-x)$ and $|f(x)|$) with those that change the sign (like $-f(x)$).
- Not remembering that $e^x$ is always positive, which can lead to the wrong conclusion about expressions involving it.
AI-generated content may contain errors. Please verify critical information