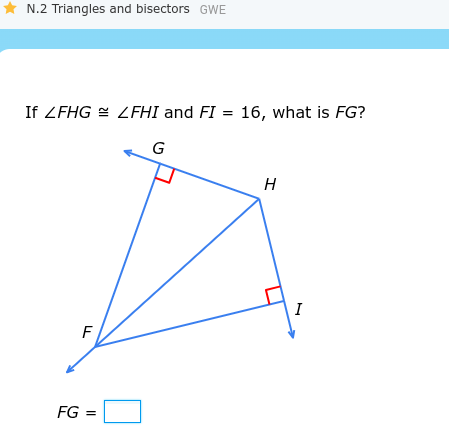
If ∠FHG ≅ ∠FHI and FI = 16, what is FG?
Understand the Problem
The problem states that angle FHG is congruent to angle FHI, and FI equals 16. We are asked to find the length of FG. Since FH bisects angle GHI, and FG and FI are perpendicular, by the Angle Bisector Theorem, FG = FI.
Answer
$FG = 16$
Answer for screen readers
$FG = 16$
Steps to Solve
- Identify the given information
We are given that $\angle FHG \cong \angle FHI$ and $FI = 16$. We also observe from the diagram that $FG$ and $FI$ are perpendicular to $HG$ and $HI$ respectively.
- Apply the Angle Bisector Theorem
The Angle Bisector Theorem states that if a point lies on the bisector of an angle, then it is equidistant from the sides of the angle. Since $FH$ bisects $\angle GHI$, and $FG$ and $FI$ are perpendicular distances from $F$ to the sides $HG$ and $HI$ respectively, then $FG = FI$.
- Substitute the value of FI
We are given that $FI = 16$. Therefore, $FG = 16$.
$FG = 16$
More Information
The Angle Bisector Theorem is a useful tool in geometry for relating the lengths of sides of a triangle to the bisector of an angle.
Tips
A common mistake is not recognizing that $FG$ and $FI$ are perpendicular to the sides of the bisected angle, which is a requirement for applying the Angle Bisector Theorem in this context.
AI-generated content may contain errors. Please verify critical information