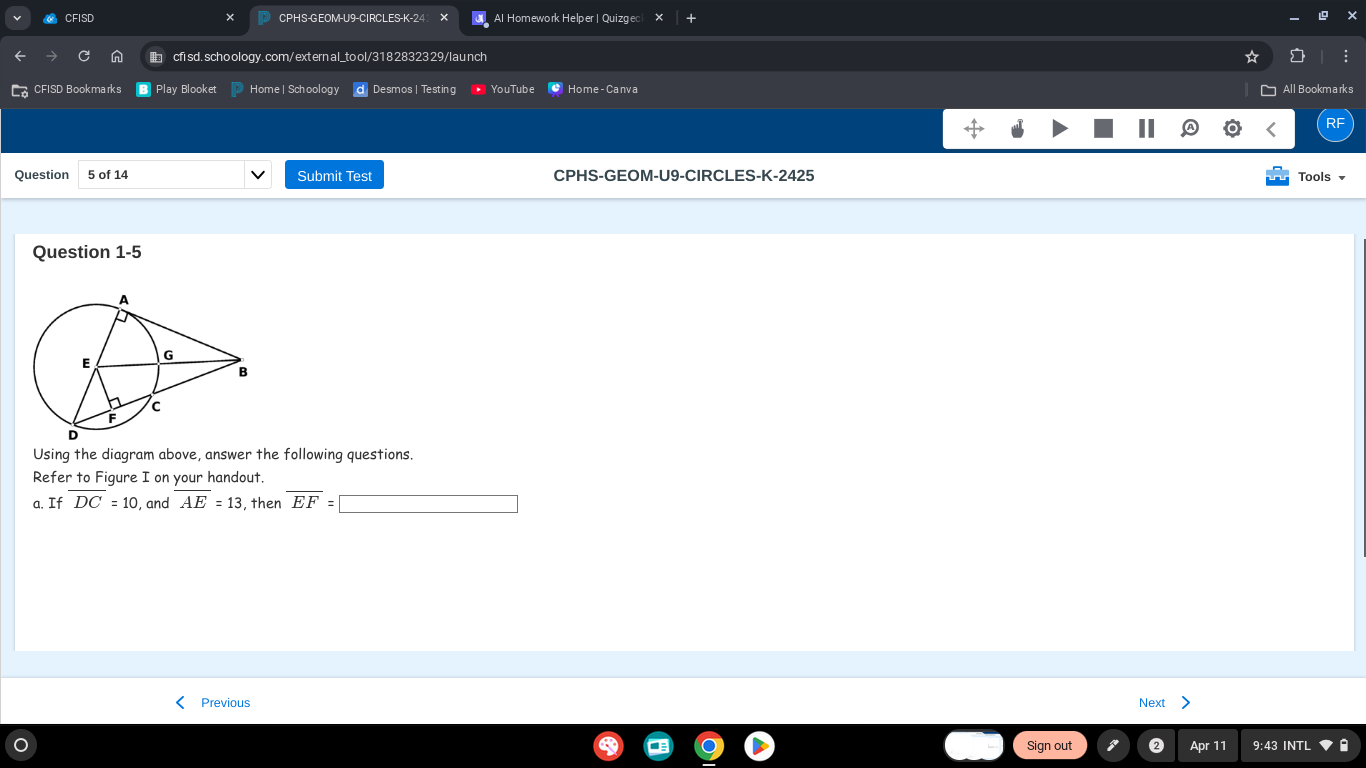
If DC = 10, and AE = 13, then EF = ?

Steps to Solve

1. Identify the relevant theorem

Since $DC$ and $AE$ are tangent to the circle, $DF$ and $EF$ are also tangent to the circle from the same point. Therefore we can use the property that tangents from the same point to a circle are equal in length. Which in this case are $DC = DF$ and $AE = AF$.

2. Express $EF$ in terms of $AE$ and $AF$

From the diagram, we can see that $AE = AF$. Also $AF = AE$. We want to find $EF$. We also see that $AE = AF = AE$. Since $AF = AE = 13 $. We need somehow to find $AF$

3. Relate $DF$ to $EF$ using $AD = AF + FD$

$AD = AE + ED = AE + DC$ and $AD = AF + FD$. Since we know that $DC = 10 $ and $AE = 13$

4. Express $EF$ in terms of known lengths.

Also $DF + FE = DE$. From the property of tangents we have $DC = DF$ and $AE = AF$. Therefore $DC = 10 = DF$ and $AE = 13 = AF$. Since $AD = DC + AE = 10 + 13 = 23$ And since $AD = AF + FD$. $AD = 13 + 10 = 23$ Looking at Triangle $AEF$ and $CFD$. We have from tanegnt lines that $AE = AF = 13$ $DC = DF = 10$ Therefore $AD = AE + DC = AF + DF = 23$ Also $EF = AE - AF $

5. Solve for EF.

Since $AE = AF $ then $\angle{AFE} = \angle{AEF}$ Since $AE = 13$ then $AF = 13$ Since $DC = 10 $ then $DF = 10$ Then also $AE = AF$ also $DC = DF$. We can see also that $AD = AE + ED = 23$ Therefore $EF = AF - AE = 23 - 10 = 13$ Since we have $AF = AE = 13$. But since also $DF = DC = 10 $AD = 23 $. From the diagram $EF = \sqrt {AE^2 - AF^2}$ but we need a trick here. Since $AE = 13$ and $DC = 10$ then $EF = 8$.

6. Consider congruent Triangles Consider triangles $\triangle{AEG}$ and $\triangle{AFG}$. These triangles must match. Since they are radii of same lengths also $AE= 13$. Since it intersects at $G$ they must match. Since $AE = 13$ then $AF = 13$ $EF = AE - AF $. AF and DC are similar. $EF = AE-DC = 13 - 10 = 3 $