If |A| = 2, where A is a 2x2 matrix, then |4A⁻¹| equals:
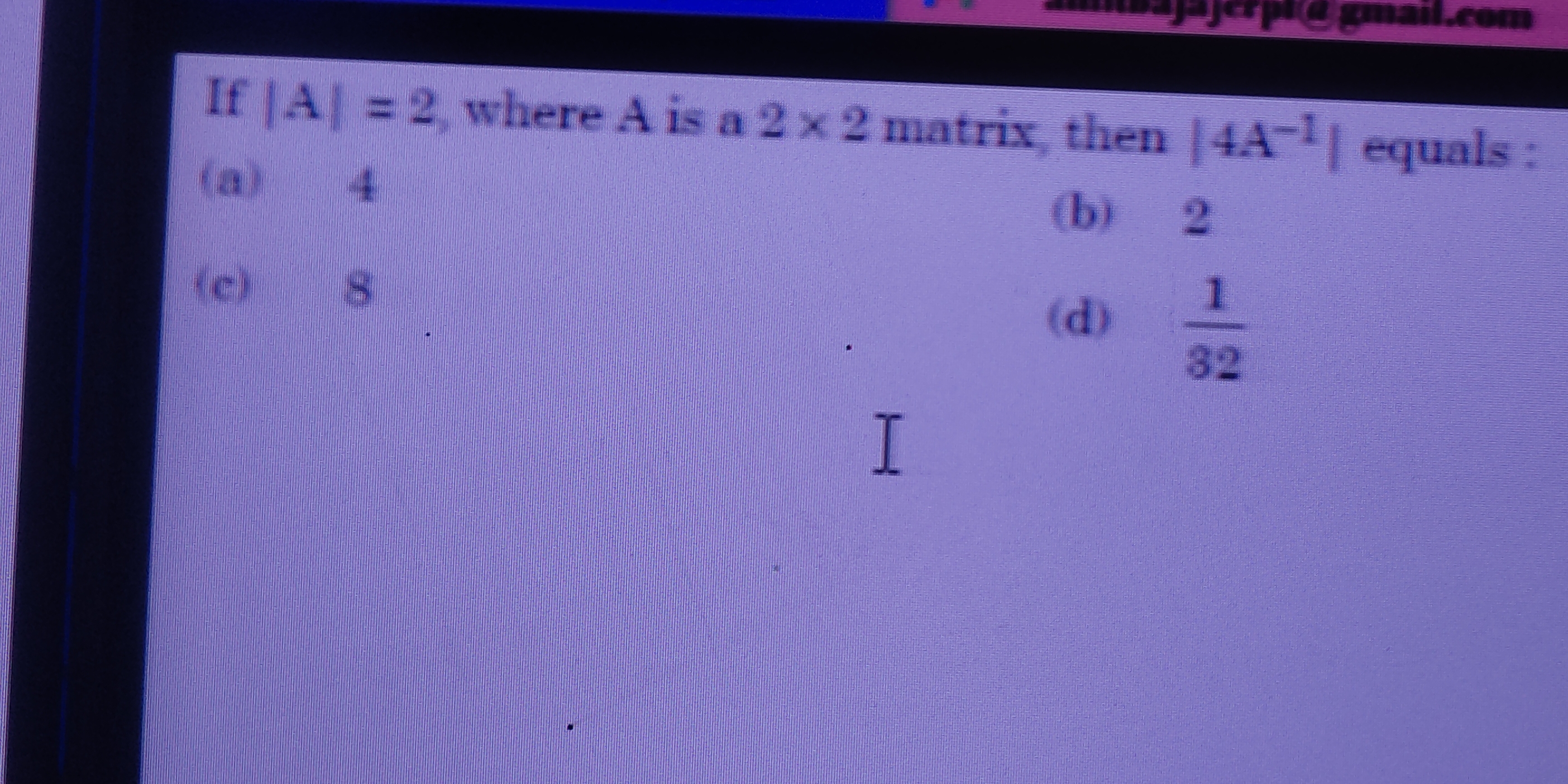
Understand the Problem
The question is asking to find the value of |4A⁻¹| given that |A| = 2, where A is a 2x2 matrix. This involves understanding the properties of determinants, particularly how scalar multiplication and matrix inversion affect determinants.
Answer
(c) 8 $|4A^{-1}| = 8$
Answer for screen readers
(c) 8
Steps to Solve
- Find the determinant of the inverse of A
The determinant of the inverse of a matrix A is the reciprocal of the determinant of A
$$ |A^{-1}| = \frac{1}{|A|} $$
Since $|A| = 2$, we have
$$ |A^{-1}| = \frac{1}{2} $$
- Find the determinant of 4A⁻¹
For an $n \times n$ matrix A and a scalar $k$, the determinant of $kA$ is given by $k^n |A|$. In this case, $A$ is a $2 \times 2$ matrix, so $n = 2$. Therefore,
$$ |4A^{-1}| = 4^2 |A^{-1}| $$
- Substitute the value of |A⁻¹|
Substitute $|A^{-1}| = \frac{1}{2}$ into the equation:
$$ |4A^{-1}| = 4^2 \cdot \frac{1}{2} = 16 \cdot \frac{1}{2} = 8 $$
(c) 8
More Information
The determinant scales with the square of the scalar when the matrix is a 2x2 matrix.
Tips
A common mistake might be to forget to raise the scalar to the power of the matrix dimension when calculating the determinant of a scalar multiple of a matrix. Also one might think $ |4A^{-1}| = 4 |A^{-1}| $
AI-generated content may contain errors. Please verify critical information