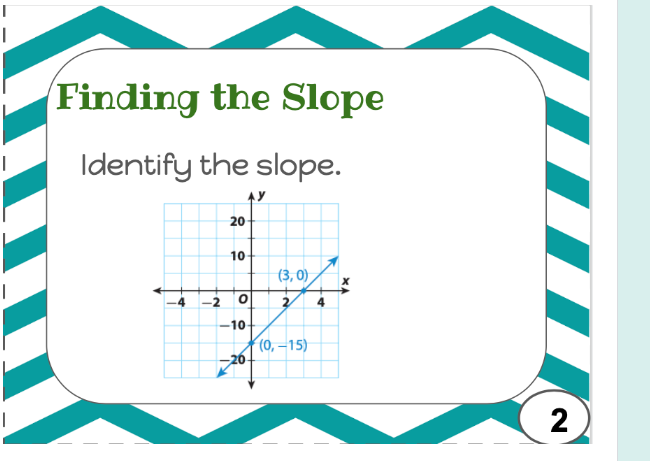
Identify the slope.
Understand the Problem
The question is asking to identify the slope of the line represented on the graph. To determine the slope, we will use the two given points on the line: (0, -15) and (3, 0). The slope formula, m = (y2 - y1) / (x2 - x1), will be applied to calculate the slope.
Answer
The slope of the line is $m = 5$.
Answer for screen readers
The slope of the line is $m = 5$.
Steps to Solve
-
Identify the points The two points given on the line are: $ (x_1, y_1) = (0, -15) $ and $ (x_2, y_2) = (3, 0) $.
-
Apply the slope formula The slope formula is given by: $$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
-
Substitute the values into the formula Substituting the values from the points into the slope formula: $$ m = \frac{0 - (-15)}{3 - 0} $$
-
Simplify the expression Simplifying the expression gives: $$ m = \frac{0 + 15}{3} = \frac{15}{3} = 5 $$
-
Final Answer The slope of the line is 5.
The slope of the line is $m = 5$.
More Information
The slope represents the rate of change of the line. Here, a slope of 5 means for every 1 unit increase in x, the value of y increases by 5 units. This indicates that the line is steep and rises as you move from left to right.
Tips
- Confusing the order of points in the formula which can lead to incorrect signs in calculations. Always use the correct order: $(x_1, y_1)$ and $(x_2, y_2)$.
AI-generated content may contain errors. Please verify critical information