Identify the graph of y < -3x + 1.

Understand the Problem

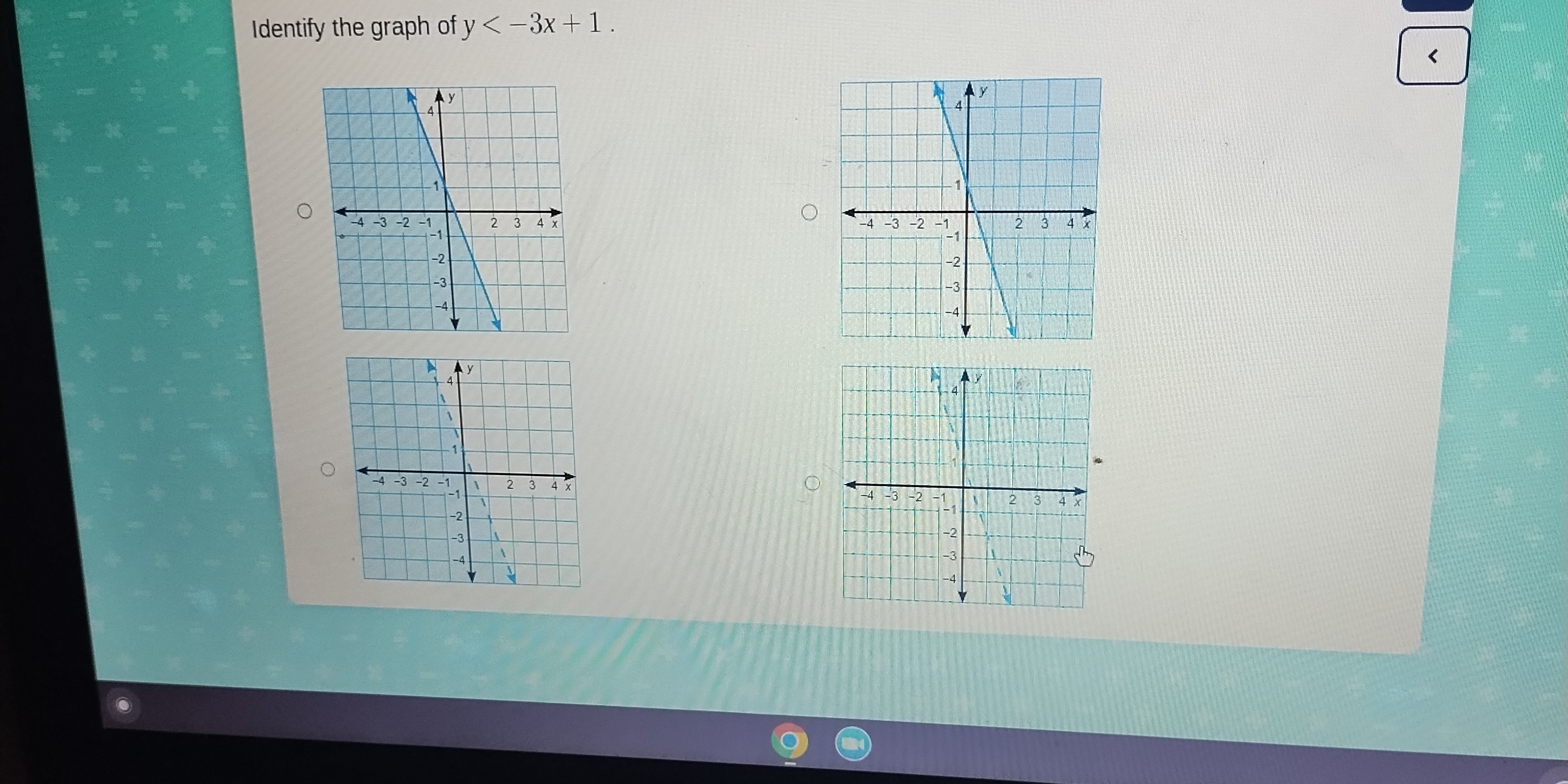
The question is asking to identify the correct graph for the inequality y < -3x + 1. This involves understanding the representation of inequalities on a graph, particularly how the line y = -3x + 1 is drawn and how the area below this line is shaded to indicate the solutions to the inequality.

Answer

The correct graph is the one with a dashed line for $ y = -3x + 1 $ and shading below the line.

Steps to Solve

Identify the Equation of the Line

The inequality is ( y < -3x + 1 ). The line we need to graph is ( y = -3x + 1 ).
Determine Key Points of the Line

To plot the line, identify two points.
- When ( x = 0 ): $$ y = -3(0) + 1 = 1 \quad \text{(Point: (0, 1))} $$
- When ( x = 1 ): $$ y = -3(1) + 1 = -2 \quad \text{(Point: (1, -2))} $$
Plot the Line

Plot the points (0, 1) and (1, -2) on the graph. Draw a dashed line through these points because the inequality is strict (<), meaning points on the line are not included in the solution.
Shade the Correct Area

Since the inequality is ( y < -3x + 1 ), shade the area below the dashed line, representing all the values where ( y ) is less than the line.
Identify the Correct Graph

Compare the graphs provided in the question with the one identified. Look for a dashed line with shading below it corresponding to the equation ( y < -3x + 1 ).

The correct graph is the one that shows a dashed line representing ( y = -3x + 1 ) with shading below the line.

More Information

The inequality ( y < -3x + 1 ) indicates that the solutions are all points where ( y ) values are less than those on the line. The slope of -3 means that for every unit the x-coordinate increases, the y-coordinate decreases by 3.

Tips

Forgetting to use a dashed line for strict inequalities (like <).
Shading the wrong side of the line. Remember that you shade below the line for ( y < ) and above for ( y > ).

AI-generated content may contain errors. Please verify critical information

Thank you for voting!