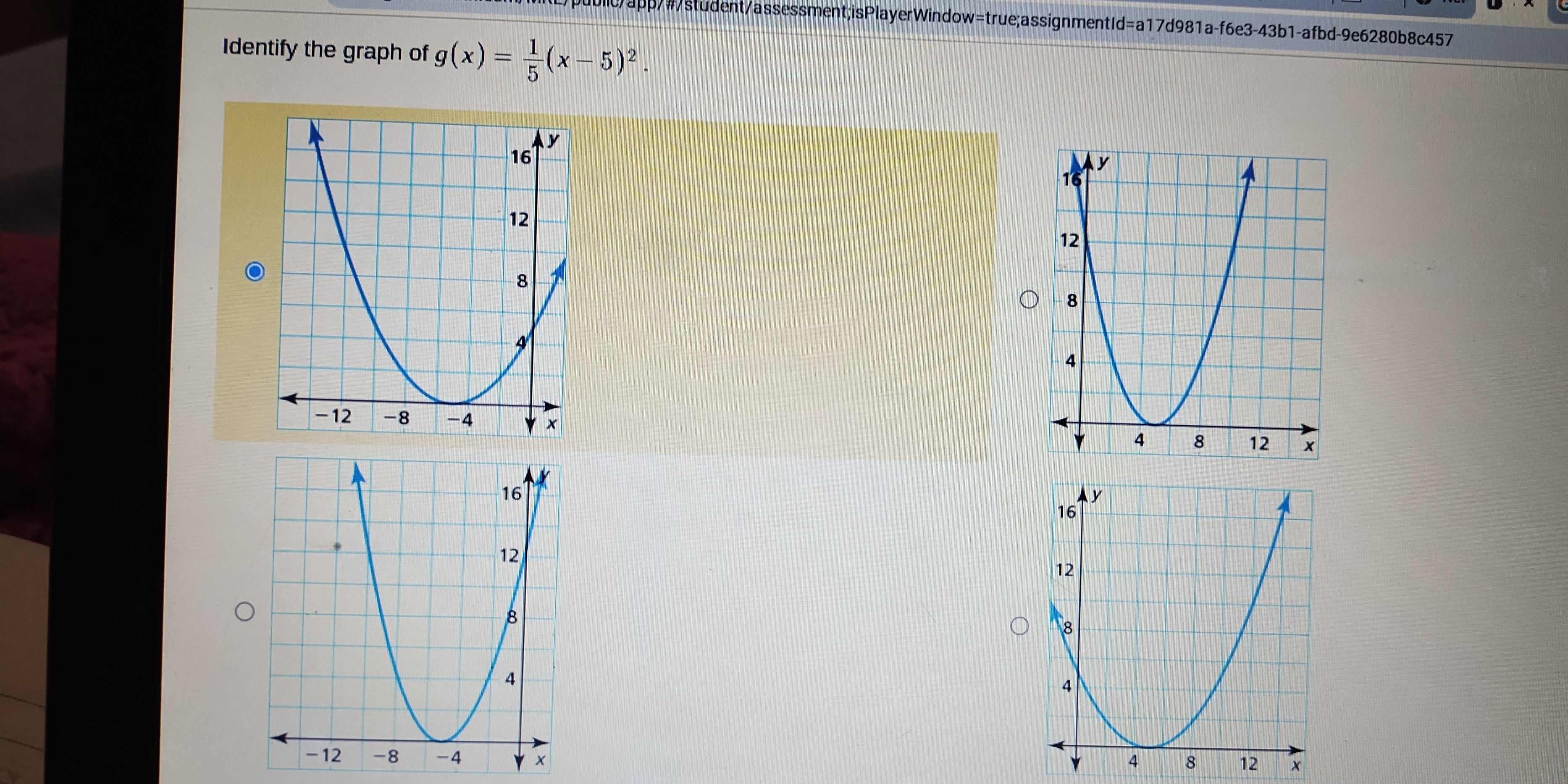
Identify the graph of g(x) = (1/5)(x-5)^2.
Understand the Problem
The question asks to identify the correct graph that matches the given quadratic function. The function is in vertex form, which helps determine the vertex and direction of the parabola.
Answer
The graph of $g(x) = \frac{1}{5}(x-5)^2$ is the one with a vertex at $(5,0)$ opening upwards.
Answer for screen readers
The correct graph is the one with the vertex at $(5, 0)$ and opening upwards.
Steps to Solve
-
Identify the vertex of the parabola. The given function is in vertex form: $g(x) = a(x - h)^2 + k$, where $(h, k)$ is the vertex of the parabola. In this case, $g(x) = \frac{1}{5}(x - 5)^2$, so $h = 5$ and $k = 0$. The vertex is therefore at $(5, 0)$.
-
Determine the direction of the parabola. The coefficient $a$ in the vertex form determines whether the parabola opens upwards or downwards. Here, $a = \frac{1}{5}$, which is positive, indicating that the parabola opens upwards.
-
Consider the effect of $a$ on the width of the parabola. Since $a = \frac{1}{5}$, which is between 0 and 1, the parabola is wider than the standard parabola $y = x^2$.
-
Examine the given graphs. We look for a parabola that opens upwards, has a vertex at $(5, 0)$, and is wider than the standard parabola.
-
Select the correct graph. The graph that satisfies these conditions has its vertex at $x=5$ and opens upward.
The correct graph is the one with the vertex at $(5, 0)$ and opening upwards.
More Information
The vertex form of a quadratic equation $y = a(x - h)^2 + k$ makes it easy to determine the vertex $(h, k)$. The sign of $a$ determines the direction of the parabola (upward if positive, downward if negative), and the magnitude of $a$ affects the parabola's width.
Tips
A common mistake is to misidentify the vertex from the equation. Remember that in the vertex form $a(x - h)^2 + k$, the vertex is $(h, k)$, not $(-h, k)$. Another mistake is to confuse the effect of the coefficient 'a' on the width of the parabola. If $0 < |a| < 1$, the parabola is wider; if $|a| > 1$, the parabola is narrower.
AI-generated content may contain errors. Please verify critical information