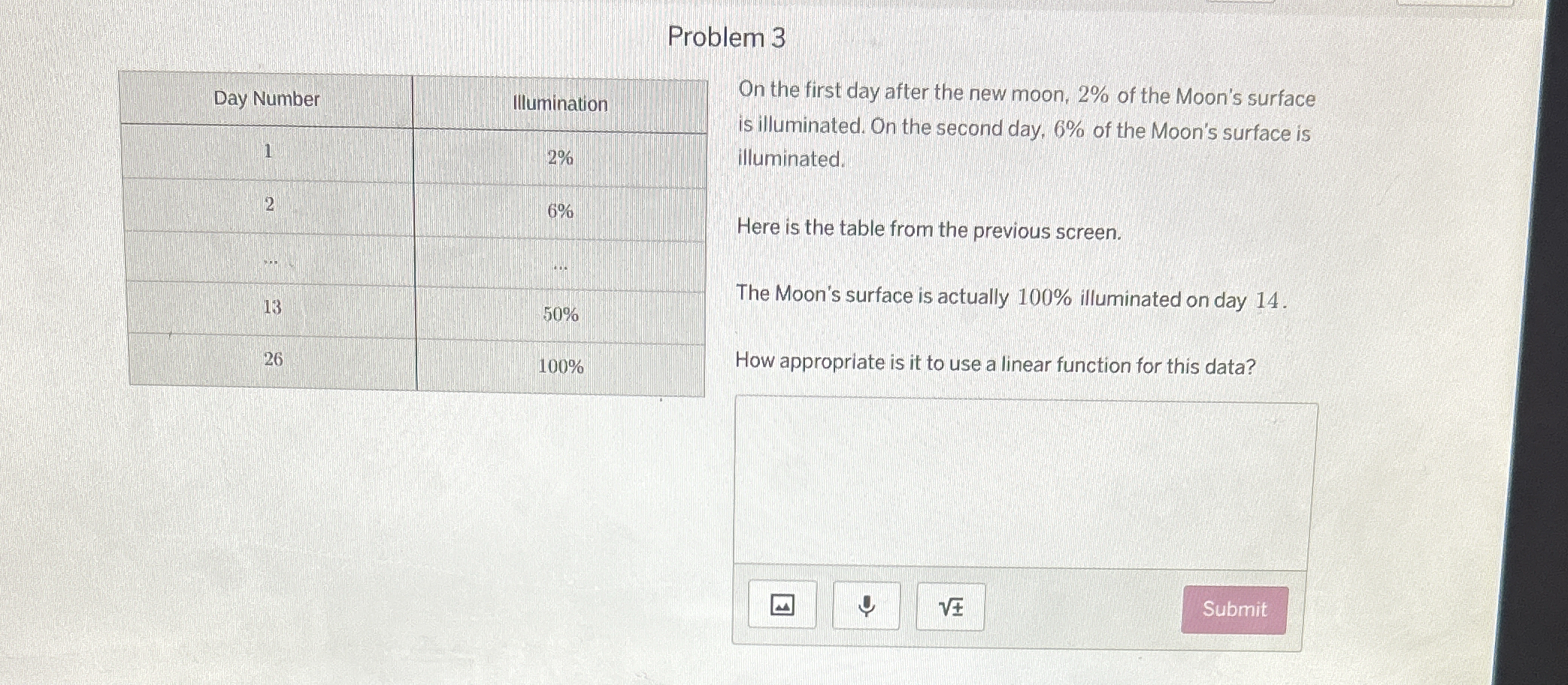
How appropriate is it to use a linear function for this data?
Understand the Problem
The question is asking us to determine the suitability of using a linear function to model the illumination percentage of the moon over a 26 day period, given data points for days 1, 2, 13, and 26. To determine this, you'll need to consider whether the data points suggest a roughly constant rate of change in illumination percentage over time.
Answer
Not appropriate, the rate of change is not constant.
Answer for screen readers
It is not appropriate to use a linear function for this data due to the rate of change not being constant.
Steps to Solve
- Calculate the rate of change between day 1 and day 2
To determine how appropriate a linear function is, we need to examine if the rate of change is approximately constant. Let's start by calculating the rate of change between day 1 and day 2.
Rate of change = $\frac{\text{Change in illumination}}{\text{Change in day number}} $
Rate of change = $\frac{6% - 2%}{2 - 1} = \frac{4%}{1} = 4%$ per day
- Calculate the rate of change between day 2 and day 13.
Rate of change = $\frac{50% - 6%}{13 - 2} = \frac{44%}{11} = 4%$ per day
- Calculate the rate of change between day 13 and day 26.
Rate of change = $\frac{100% - 50%}{26 - 13} = \frac{50%}{13} \approx 3.85%$ per day
- Assess the suitability of a linear model
The rates of change are $4%$, $4%$, and $3.85%$. Since these values are close but not exactly the same, we need to consider that a linear model may not be perfectly appropriate, but it could still be a reasonable approximation. Furthermore, the problem states that the moon is $100%$ illuminated on day $14$. This is another data point to consider. If we use the points $(1, 2%)$ and $(14, 100%)$ to find the slope we get:
$m = \frac{100% - 2%}{14 - 1} = \frac{98%}{13} \approx 7.54%$
Having a rate of change of $7.54%$ between days 1 and 14, then a subsequent rate of change from days 13 to 26 of $3.85%$ demonstrates that the rate of change isn't constant and therefore a linear function is not appropriate for this data.
It is not appropriate to use a linear function for this data due to the rate of change not being constant.
More Information
The lunar cycle, which includes the phases of the moon, is periodic but not perfectly linear. Tidal forces and orbital mechanics influence the exact timing and illumination.
Tips
A common mistake is only considering the first few data points and not recognizing that the rate of change varies significantly across the entire 26-day period. Another mistake is not remembering the information regarding illumination percentage on day $14$.
AI-generated content may contain errors. Please verify critical information