حل في R المعادلة (2x-4)(-5x+15)≤0
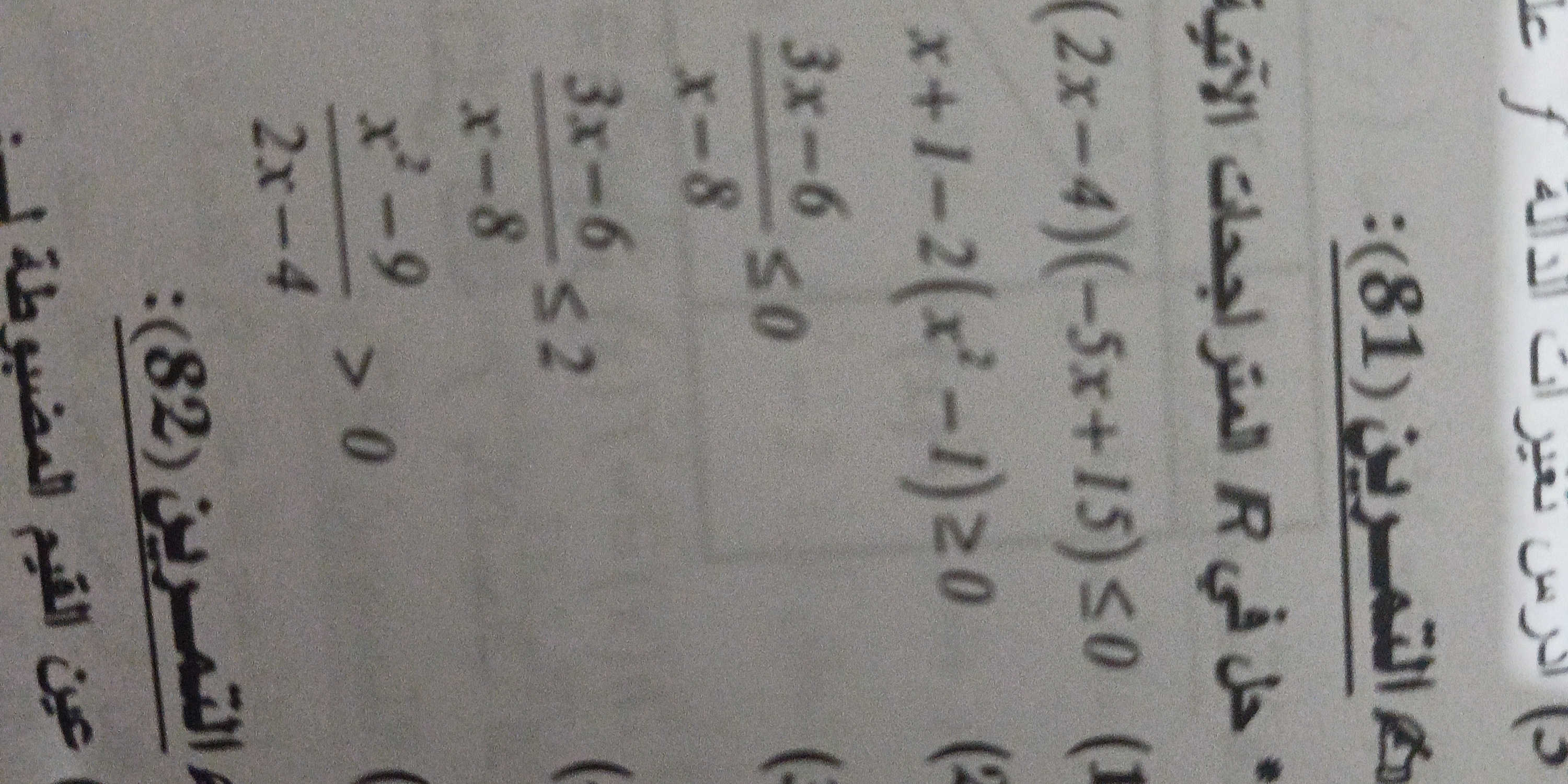
Understand the Problem
السؤال يطلب منا حل معادلة رياضية تتعلق بتحديد القيم التي تجعل عبارة رياضية معينة أقل من أو تساوي صفر.
Answer
$$2 \leq x \leq 3$$
Answer for screen readers
الجواب هو: $$2 \leq x \leq 3$$
Steps to Solve
-
فك المعادلة نبدأ بفك المعادلة المعطاة: $$(2x - 4)(-5x + 15) \leq 0$$
-
تحديد القيم الحرجة نجد القيم الحرجة للمعادلة، حيث يمكن العثور عليها من المعادلة بتعيين كل عامل يساوي صفر:
- $2x - 4 = 0 \implies x = 2$
- $-5x + 15 = 0 \implies x = 3$
- تحديد الفترات نلاحظ أن لدينا القيم الحرجة $x = 2$ و$x = 3$. نقسم محور $x$ لفترات:
- $(-\infty, 2)$
- $(2, 3)$
- $(3, +\infty)$
- اختبار القيم في الفترات نختبر كل فترة باستخدام قيمة عشوائية لتحديد إشارتها:
- فترة $(-\infty, 2)$: نختار $x = 0$: $$(2(0)-4)(-5(0)+15) = (-4)(15) = -60 \leq 0$$
- فترة $(2, 3)$: نختار $x = 2.5$: $$(2(2.5)-4)(-5(2.5)+15) = (1)(-7.5) = -7.5 \leq 0$$
- فترة $(3, +\infty)$: نختار $x = 4$: $$(2(4)-4)(-5(4)+15) = (4)(-5) = -20 \leq 0$$
- إدراج القيم الحرجة بما أن التعبير يكون صفرًا عند $x = 2$ و$x = 3$، يجب تضمين هاتين النقطتين في الحل: $$2 \leq x \leq 3$$
الجواب هو: $$2 \leq x \leq 3$$
More Information
هذه المعادلة تمثل فترة حيث يكون الناتج مطلوبًا أن يكون أقل من أو يساوي صفر. استخدام العوامل يساعد في تحديد الفترات بشكل فعال دون الحاجة إلى توسيع المعادلة بالكامل.
Tips
- إغفال القيم الحرجة: يجب دائمًا التفكير في القيم حيث المعادلة تساوي صفر.
- عدم اختبار جميع الفترات: التأكد من اختبار جميع الفترات الناتجة عن القيم الحرجة لتحديد الإشارات بشكل صحيح.
AI-generated content may contain errors. Please verify critical information