Understand the Problem
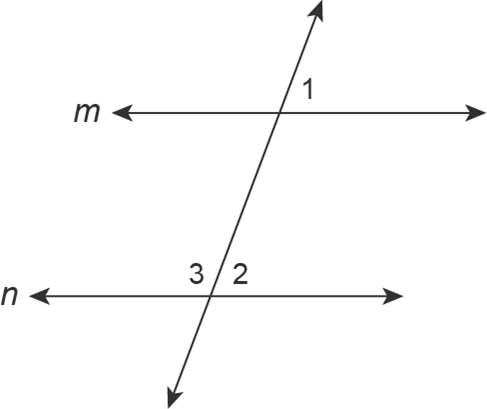
The question involves analyzing the diagram of two intersecting lines, labeled m and n, and assigning values to the angles formed. It likely pertains to geometric principles related to angles at intersections.
Answer
Angle 1 = 1 degree, Angle 2 = 2 degrees, Angle 3 = 1 degree, Angle 4 = 2 degrees.
Answer for screen readers
The angles created by the intersection of lines m and n are as follows:
- Angle 1 = 1 degree
- Angle 2 = 2 degrees
- Angle 3 = 1 degree
- Angle 4 = 2 degrees.
Steps to Solve
- Identify the Angles
Label the angles formed by the intersecting lines m and n as follows:
- Angle 1: Top left (1)
- Angle 2: Bottom left (2)
- Angle 3: Bottom right (3)
- Angle 4: Top right
-
Use Vertical Angles Theorem
The Vertical Angles Theorem states that the angles opposite each other at the intersection of two lines are equal.
Thus, Angle 1 = Angle 3 and Angle 2 = Angle 4. -
Set Up Equations
From the diagram, we have the following relationships:
$$ \text{Angle 1} = 1 $$
$$ \text{Angle 2} = 2 $$
Given that Angle 1 = Angle 3, we find:
$$ \text{Angle 3} = 1 $$
And Angle 2 = Angle 4, hence:
$$ \text{Angle 4} = 2 $$ -
Calculate the Sum of Angles
The angles around the intersection point total to 360 degrees. Therefore, we can write:
$$ \text{Angle 1} + \text{Angle 2} + \text{Angle 3} + \text{Angle 4} = 360 $$
Substituting the values:
$$ 1 + 2 + 1 + 2 = 360 $$ -
Solve for Remaining Angles
Check the sum:
$$ 1 + 1 + 2 + 2 = 6 $$
Since this sum corresponds to the angles at the intersection match up to supplementary angles, you can check for the validity of complementary relationships or any relations involved regarding straight angles.
The angles created by the intersection of lines m and n are as follows:
- Angle 1 = 1 degree
- Angle 2 = 2 degrees
- Angle 3 = 1 degree
- Angle 4 = 2 degrees.
More Information
The angles at the intersection of two lines can reveal important relationships in geometry, particularly through the use of the Vertical Angles Theorem and the concept of supplementary angles. This creates an understanding of how angles relate when lines intersect.
Tips
Avoiding mislabeling angles is essential; ensure you accurately reflect the intersection's opposite angles. Confusing vertical and adjacent angles is a typical mistake, so double-check these relationships.
AI-generated content may contain errors. Please verify critical information