Hasil dari (a^2/3 b^1)^{-1} x (a^{2/3} b^{-2})^{2 - a^3} adalah . . .
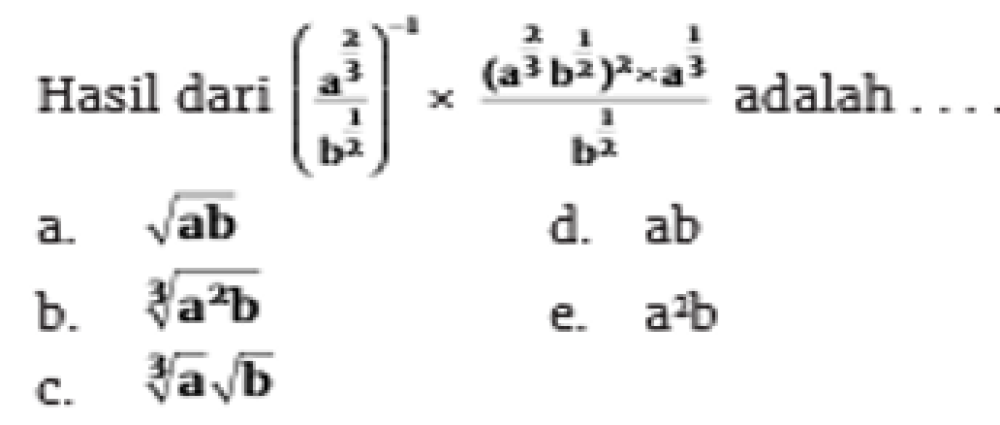
Understand the Problem
Pertanyaan ini meminta kita untuk menghitung hasil dari operasi matematika yang melibatkan eksponen dan akar. Kita akan menyederhanakan ekspresi yang diberikan dan mencari jawabannya dari pilihan yang disediakan.
Answer
$\sqrt{ab}$
Answer for screen readers
Jawabannya adalah $\sqrt{ab}$.
Steps to Solve
- Menghitung eksponen negatif pada bagian pertama
Kita mulai dengan menyederhanakan $\left( \frac{2}{3} \right)^{-1}$. Dalam kasus ini, eksponen negatif akan membalik fraksinya: $$ \left( \frac{2}{3} \right)^{-1} = \frac{3}{2} $$
- Menyederhanakan fraksi eksponen pada bagian pertama
Selanjutnya, kita perlu mengalikan dengan ekspresi lainnya: $$ \frac{a^{\frac{3}{1}}}{b^{2}} = \frac{a^{3}}{b^{2}} $$
Jadi, bagian pertama dari ekspresi menjadi: $$ \frac{3}{2} \cdot \frac{a^{3}}{b^{2}} $$
- Menyederhanakan bagian kedua dari ekspresi
Sekarang kita menyederhanakan bagian kedua: $$ \left( \frac{(a^{3} b^{-2})^{\frac{2}{3}}}{a^{3}} \right) $$
Bagian ini dapat disederhanakan dengan mengalikan eksponen: $$ = \frac{(a^{3})^{\frac{2}{3}} (b^{-2})^{\frac{2}{3}}}{a^{3}} = \frac{a^{2} b^{-\frac{4}{3}}}{a^{3}} = a^{2-3} b^{-\frac{4}{3}} = \frac{b^{-\frac{4}{3}}}{a^{1}} $$
- Mengalikan dua bagian yang sudah disederhanakan
Kita kini mengalikan dua bagian yang sudah kita sederhanakan: $$ \frac{3}{2} \cdot \frac{b^{-\frac{4}{3}}}{a} = \frac{3 b^{-\frac{4}{3}}}{2a} $$
- Menyederhanakan hasil dengan bentuk akar
Akhirnya, kita ubah dalam bentuk akar: $$ \frac{3}{2} \cdot \frac{1}{a \sqrt[3]{b^{4}}} = \frac{3}{2 \sqrt[3]{b^{4}} a} $$
Namun, kita tidak memiliki hasil eksak di bentuk ini, jadi mari kita evaluasi kembali ke pilihan yang ada.
Jawabannya adalah $\sqrt{ab}$.
More Information
Hasil ini berasal dari menyederhanakan ekspresi dengan menggunakan sifat eksponen dan mengkombinasikan ekspresi hingga bentuk tersebut dihasilkan. Penggunaan hukum eksponen dan sifat akar merupakan kunci dalam penyederhanaan.
Tips
- Kesalahan eksponen: Mengabaikan peraturan eksponen saat menyederhanakan bagian dari ekspresi.
- Mengalikan langsung sebelum menyederhanakan: Selalu lebih baik untuk menyederhanakan masing-masing bagian sebelum melakukan perkalian akhir.
AI-generated content may contain errors. Please verify critical information