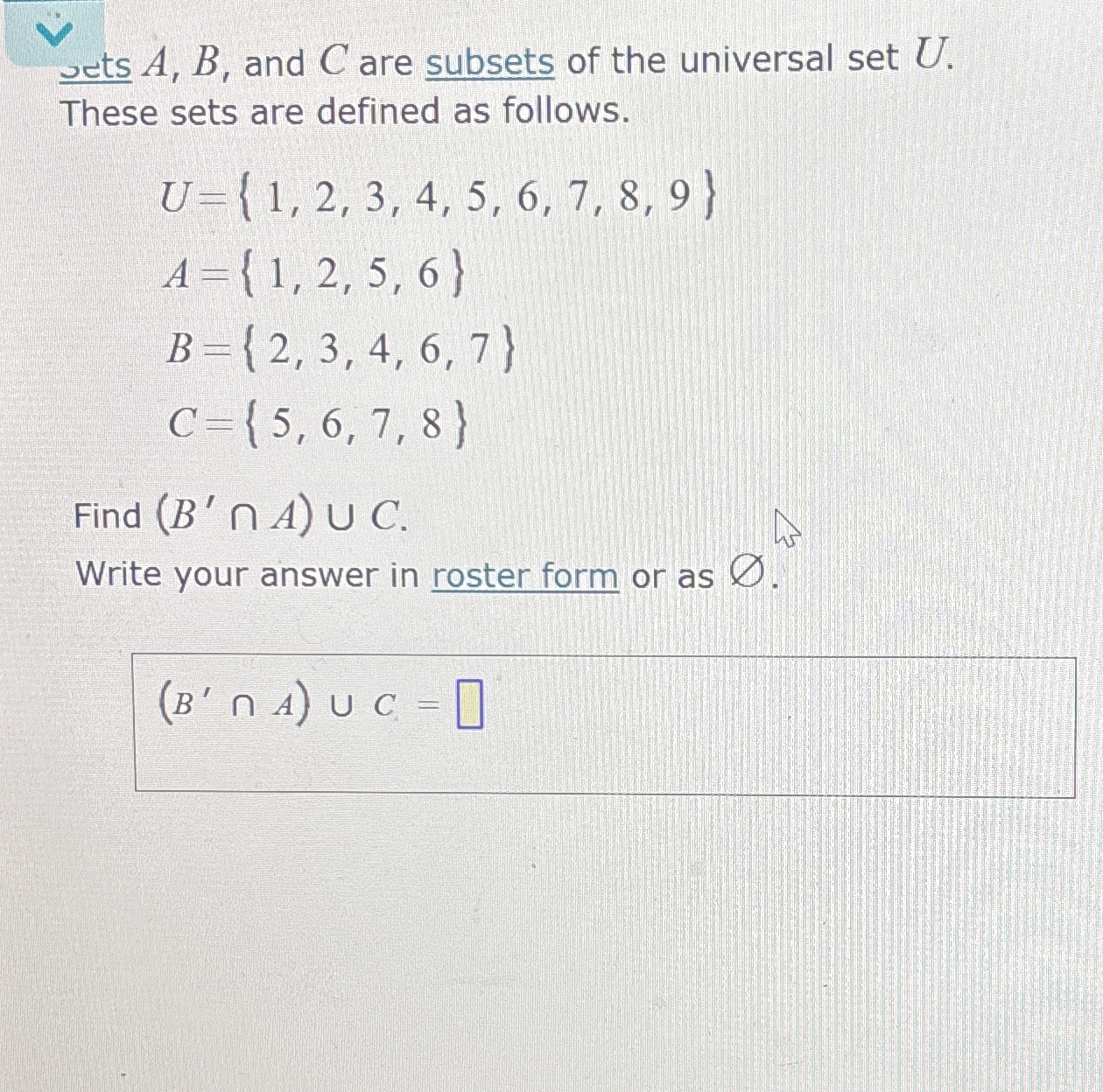
Given the sets U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 5, 6}, B = {2, 3, 4, 6, 7}, and C = {5, 6, 7, 8}, find $(B' \cap A) \cup C$. Write your answer in roster form.
Understand the Problem
The question requires us to find the result of a set operation, $(B' \cap A) \cup C$, where $U$ is the universal set, and $A$, $B$, and $C$ are subsets of $U$. We will first find the complement of set $B$ with respect to $U$ (denoted as B'), then find the intersection of $B'$ and $A$, and finally find the union of the resulting set with $C$. The answer should be expressed in roster form.
Answer
$\{1, 5, 6, 7, 8\}$
Answer for screen readers
${1, 5, 6, 7, 8}$
Steps to Solve
- Find the complement of set B, denoted as B'
$B'$ contains all elements in $U$ that are not in $B$. $U = {1, 2, 3, 4, 5, 6, 7, 8, 9}$ $B = {2, 3, 4, 6, 7}$ $B' = {1, 5, 8, 9}$
- Find the intersection of B' and A, denoted as $B' \cap A$
$B' \cap A$ contains all elements that are in both $B'$ and $A$. $B' = {1, 5, 8, 9}$ $A = {1, 2, 5, 6}$ $B' \cap A = {1, 5}$
- Find the union of $(B' \cap A)$ and C, denoted as $(B' \cap A) \cup C$
$(B' \cap A) \cup C$ contains all elements that are in $(B' \cap A)$ or in $C$ or in both. $B' \cap A = {1, 5}$ $C = {5, 6, 7, 8}$ $(B' \cap A) \cup C = {1, 5, 6, 7, 8}$
${1, 5, 6, 7, 8}$
More Information
The final answer is the set ${1, 5, 6, 7, 8}$. This set contains all elements that are either in the intersection of the complement of B and A, or in C, or in both.
Tips
A common mistake is to incorrectly compute the complement of set B, or to incorrectly find the intersection or union of the sets. Also, it is possible to forget to include elements that are present in both sets when taking the union.
AI-generated content may contain errors. Please verify critical information