Given the inequalities and equalities: E ≤ C, A = B ≥ P < T = S; Q > C = I, V > C, P ≥ B = A ≥ S < T = Q; C = D < P < U; E > I, A > Q, P ≥ B = A ≥ S < T > D > R = J, I < C < P, II.... Given the inequalities and equalities: E ≤ C, A = B ≥ P < T = S; Q > C = I, V > C, P ≥ B = A ≥ S < T = Q; C = D < P < U; E > I, A > Q, P ≥ B = A ≥ S < T > D > R = J, I < C < P, II. Q > R, what are the relationships among these variables?
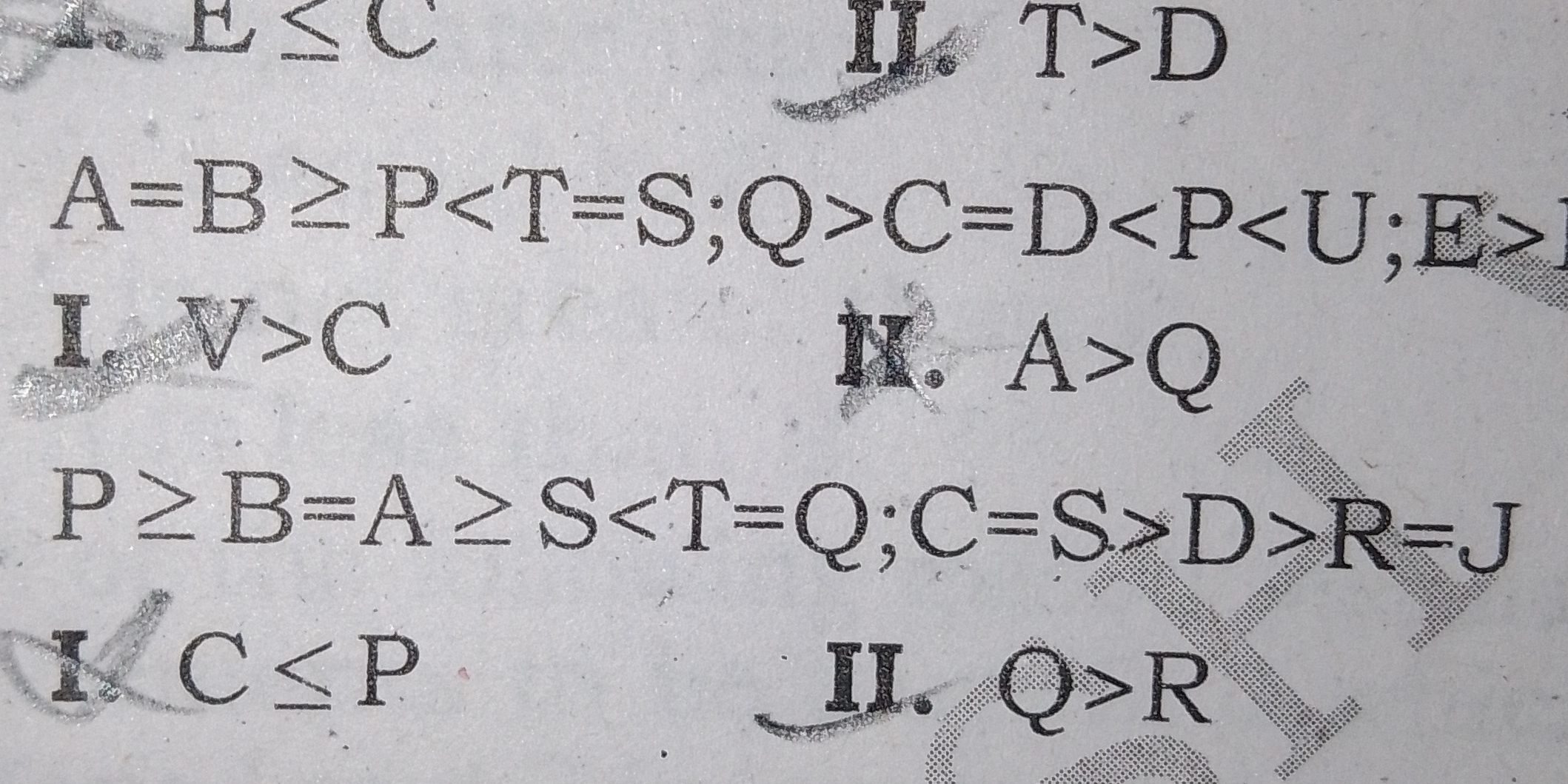
Understand the Problem
The question presents a series of inequalities and equalities involving different variables. The goal is likely to deduce the relationships between these variables based on the provided expressions.
Answer
\(Q > R\)
Answer for screen readers
From the established relationships, we can summarize:
- (V > C \geq E)
- (Q > C = I)
- (A = B \geq P < T = S > D > R = J)
Finally, based on the relationships deduced, we find that:
III: (Q > R) is true.
Steps to Solve
-
Identify Relationships from Equations Read through the given inequalities and equations to establish the relationships between the variables. For instance:
- From (E \leq C), we understand that (C) is greater than or equal to (E).
- From (A = B \geq P < T = S), we can establish (A) and (B) are equal and greater than or equal to (P), which is less than (T) and equal to (S).
-
Chain the Relationships Continue chaining the relationships established:
- From the next line (Q > C = I), we deduce that (Q) is greater than (C), thus also greater than (E) since (E \leq C).
- Continuing, (V > C) implies (V) is also greater than (E).
-
Complete the Inequalities Use the provided expressions to form a complete inequality chain:
- From previous steps, we can start to list out all established relationships:
- (V > C \geq E)
- (A = B \geq P < T = S)
- (Q > C = I)
- From previous steps, we can start to list out all established relationships:
-
Add and Solve New Relations Integrate additional inequalities to expand the comparison:
- From (P \geq B = A \geq S < T) and the previous results, we fill in the gaps:
- (P) could be equal to (B) which is equal to (A) and less than (S) and (T).
- Continue this process until all variables are connected.
- From (P \geq B = A \geq S < T) and the previous results, we fill in the gaps:
-
Check Final Relations Final verification of how (R) and (Q) relate:
- The last parts state that (S > D > R = J) and determines (P) relative to (B), confirming that (R) is linked directly to (Q) and (D).
From the established relationships, we can summarize:
- (V > C \geq E)
- (Q > C = I)
- (A = B \geq P < T = S > D > R = J)
Finally, based on the relationships deduced, we find that:
III: (Q > R) is true.
More Information
The inequalities span several variables and their relationships can form a network of comparisons. This type of problem often appears in logical reasoning tests, helping to evaluate relational understanding. The chains of inequalities can sometimes be confusing, so it is important to track each relation step-by-step.
Tips
- Missing Relationships: One common mistake is skipping over some inequalities. It’s essential to connect every piece logically.
- Incorrect Chain Order: Ensure the order of inequalities is respected; mistakenly reversing them can lead to incorrect conclusions.
- Ignoring Equalities: Remember that equal conditions should be treated carefully since they hold specific values relative to the others.
AI-generated content may contain errors. Please verify critical information