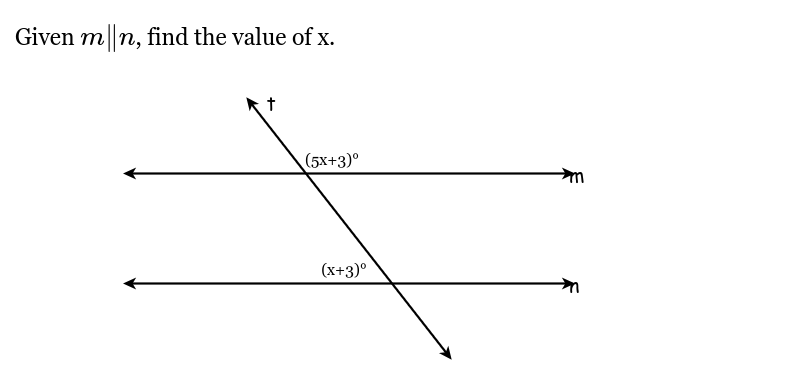
Given m || n, find the value of x.
Understand the Problem
The question is asking us to find the value of x given that lines m and n are parallel, and it provides expressions for the angles formed by a transversal intersecting these lines.
Answer
The value of \( x \) is \( 0 \).
Answer for screen readers
The value of ( x ) is ( 0 ).
Steps to Solve
- Understanding angle relationships
Since lines ( m ) and ( n ) are parallel, the angles formed by the transversal have certain relationships. The angle ( (5x + 3)^\circ ) and the angle ( (x + 3)^\circ ) are corresponding angles. Therefore, they are equal:
$$ 5x + 3 = x + 3 $$
- Setting up the equation
Now, we'll simplify the equation we set up in the previous step. To do this, we will isolate ( x ) on one side:
Subtract ( x ) from both sides:
$$ 5x + 3 - x = 3 $$
This simplifies to:
$$ 4x + 3 = 3 $$
- Solving for ( x )
Next, we will subtract ( 3 ) from both sides to isolate the term with ( x ):
$$ 4x + 3 - 3 = 3 - 3 $$
This simplifies to:
$$ 4x = 0 $$
- Final step to find ( x )
Now, divide both sides by ( 4 ) to solve for ( x ):
$$ x = \frac{0}{4} $$
Therefore:
$$ x = 0 $$
The value of ( x ) is ( 0 ).
More Information
In this problem, the concepts of parallel lines and corresponding angles are crucial. Corresponding angles are equal when a transversal intersects parallel lines. This property helps to set up the equation and solve for the unknown variable.
Tips
- A common mistake is misidentifying which angles are corresponding. It's important to ensure you are working with the correct pair of angles formed by the transversal and the parallel lines.
- Another mistake is incorrectly simplifying the equation. Always double-check each algebraic manipulation for accuracy.
AI-generated content may contain errors. Please verify critical information