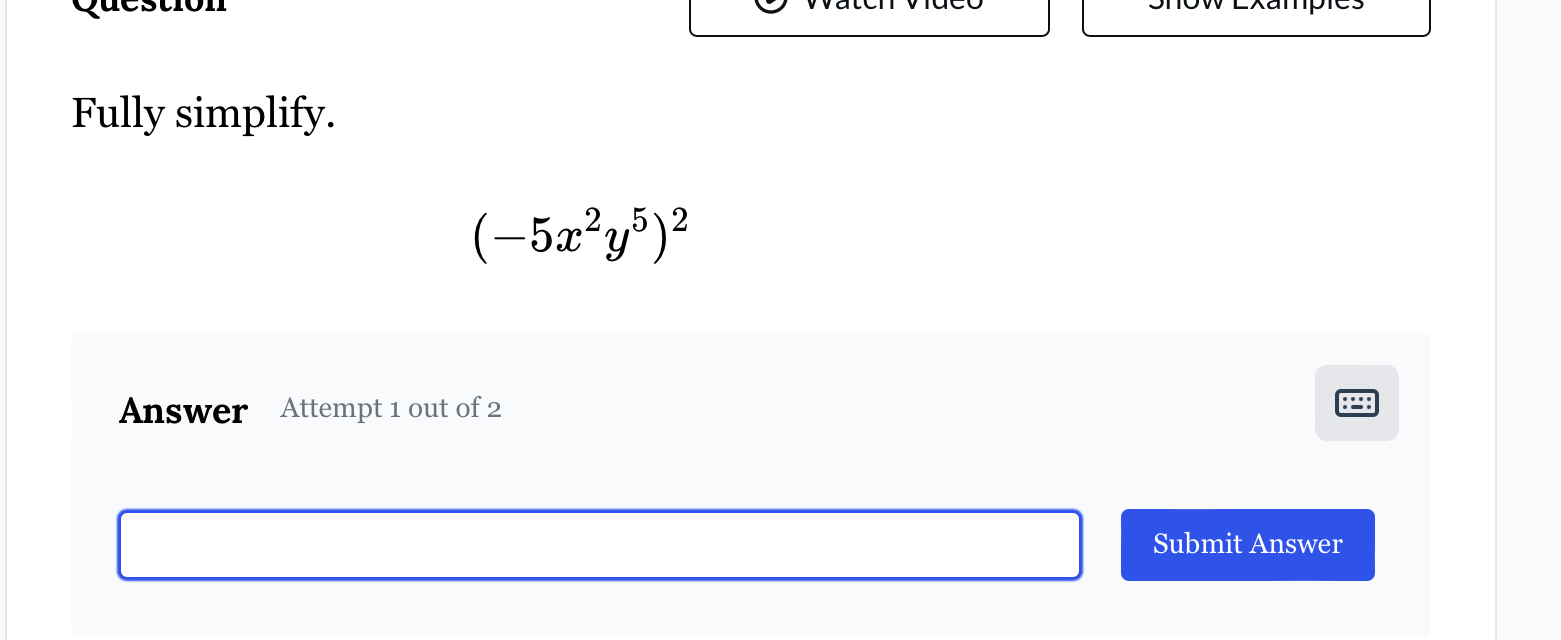
Fully simplify (−5x²y⁵)².
Understand the Problem
The question is asking to fully simplify the expression given, which is ((-5x^2y^5)^2). This involves applying the power to each factor in the expression according to the laws of exponents.
Answer
\(25 x^4 y^{10}\)
Answer for screen readers
The fully simplified expression is (25 x^4 y^{10}).
Steps to Solve
- Apply the power to the entire expression
When squaring the expression ((-5x^2y^5)^2), we apply the exponent to each part inside the parentheses: [ (-5)^2 (x^2)^2 (y^5)^2 ]
- Calculate each individual term
Now, calculate each component:
- The squared term ((-5)^2 = 25)
- The variable term ((x^2)^2 = x^{2 \cdot 2} = x^4)
- The variable term ((y^5)^2 = y^{5 \cdot 2} = y^{10})
- Combine all the results
Putting all the parts together, we have: [ 25 x^4 y^{10} ]
The fully simplified expression is (25 x^4 y^{10}).
More Information
The simplification shows how to apply exponent rules to each part of the expression. The negative sign is squared, resulting in a positive value. This process is essential in algebra when working with polynomials and compound expressions.
Tips
- Forgetting to square the negative sign: Some may neglect that squaring a negative number turns it positive.
- Incorrectly applying exponent rules: Ensure you multiply the exponents correctly while using the power of a power rule.
AI-generated content may contain errors. Please verify critical information