\( \frac{x}{x+4} - \frac{x+4}{x} < 0 \)
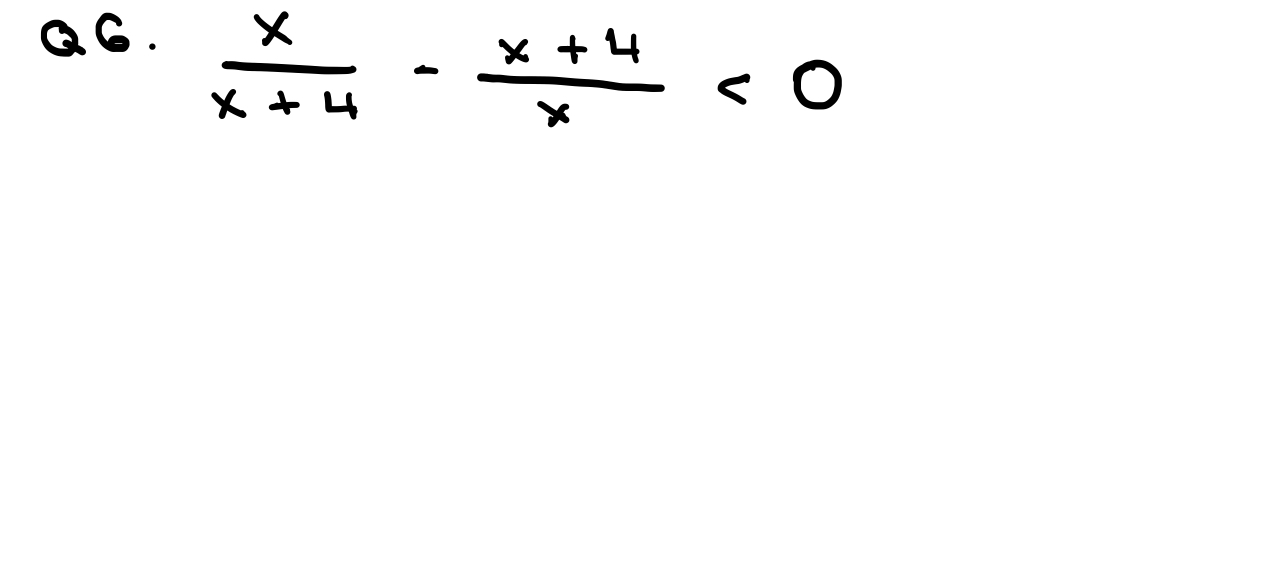
Understand the Problem
The question is asking to solve the inequality involving rational expressions. The left side of the inequality includes a subtraction of two fractions, and we need to determine for which values of x the result is less than zero.
Answer
The solution is $x \in (-\infty, -4) \cup (-4, \infty)$.
Answer for screen readers
The solution to the inequality is:
$$ x \in (-\infty, -4) \cup (-4, \infty) $$
Steps to Solve
- Common Denominator To compare the two fractions, we first find a common denominator. The common denominator for $\frac{x}{x+4}$ and $\frac{x+4}{x}$ is $x(x+4)$. We can rewrite the inequality as follows:
$$ \frac{x^2}{x(x+4)} - \frac{(x+4)(x+4)}{x(x+4)} < 0 $$
- Combine the Fractions Now, we combine the fractions over the common denominator:
$$ \frac{x^2 - (x+4)(x+4)}{x(x+4)} < 0 $$
- Expand and Simplify Next, we expand the numerator:
$$ x^2 - (x^2 + 8x + 16) < 0 $$
This simplifies to:
$$ -x^2 - 8x - 16 < 0 $$
- Rearranging We can multiply through by -1 (remembering to flip the inequality):
$$ x^2 + 8x + 16 > 0 $$
- Factoring the Quadratic The quadratic factors as:
$$ (x + 4)^2 > 0 $$
- Identifying Solutions The expression $(x + 4)^2$ is equal to 0 when $x = -4$. Since the square of a number is always non-negative, $(x + 4)^2 > 0$ for all $x$ except $x = -4$.
Thus, the solution is:
$$ x \in (-\infty, -4) \cup (-4, \infty) $$
The solution to the inequality is:
$$ x \in (-\infty, -4) \cup (-4, \infty) $$
More Information
The expression $(x + 4)^2 > 0$ implies that it will be positive for all real numbers except when the factor is zero. In this case, it is useful to identify critical points and test intervals around them.
Tips
- Forgetting to flip the inequality sign when multiplying or dividing by a negative number.
- Misfactors when expanding or combining the quadratics.
- Not identifying the correct intervals from the factors.
AI-generated content may contain errors. Please verify critical information