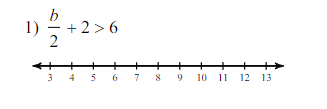
\( \frac{b}{2} + 2 > 6 \)
Understand the Problem
The question is asking to solve the inequality ( \frac{b}{2} + 2 > 6 ) and determine the values of ( b ) that satisfy this condition.
Answer
The solution is \( b > 8 \).
Answer for screen readers
The solution to the inequality is ( b > 8 ).
Steps to Solve
- Isolate the fraction
To solve the inequality ( \frac{b}{2} + 2 > 6 ), we first isolate the term with ( b ).
Subtract 2 from both sides:
[ \frac{b}{2} > 6 - 2 ]
This simplifies to:
[ \frac{b}{2} > 4 ]
- Eliminate the fraction
Next, we eliminate the fraction by multiplying both sides by 2 (remember to maintain the inequality direction since 2 is positive):
[ b > 4 \times 2 ]
This results in:
[ b > 8 ]
- Visualizing the solution
The solution means that any value of ( b ) greater than 8 will satisfy the inequality.
We can represent this on the number line with an open circle at 8 and shading to the right.
The solution to the inequality is ( b > 8 ).
More Information
This inequality tells us that ( b ) can take on any real number greater than 8, which means values like 9, 10, and so on are all valid.
Tips
- Neglecting to reverse the inequality: If you multiply or divide by a negative number, remember to flip the inequality sign. In this case, we didn't, which is good.
- Incorrect arithmetic: Make sure you accurately perform basic arithmetic operations, especially when simplifying both sides.
AI-generated content may contain errors. Please verify critical information