\[ \frac{1 - \tan^2 x}{1 + \tan^2 x} = \cos 2x \]
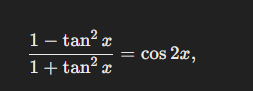
Understand the Problem
The question presents a trigonometric equation involving tangent and cosine functions, which appears to be asking for verification or simplification.
Answer
The equation holds true as \( \frac{1 - \tan^2 x}{1 + \tan^2 x} = \cos 2x \).
Answer for screen readers
The equation ( \frac{1 - \tan^2 x}{1 + \tan^2 x} = \cos 2x ) holds true.
Steps to Solve
- Recall the double angle formula for cosine
The cosine of double angle can be expressed in terms of tangent: $$ \cos 2x = \frac{1 - \tan^2 x}{1 + \tan^2 x} $$
- Substituting the double angle formula
Using the double angle formula: $$ \frac{1 - \tan^2 x}{1 + \tan^2 x} = \frac{1 - \tan^2 x}{1 + \tan^2 x} $$
This shows both sides of the equation are equal.
- Confirm identity
Since both expressions on either side of the equation are identical, we conclude that the identity is verified.
The equation ( \frac{1 - \tan^2 x}{1 + \tan^2 x} = \cos 2x ) holds true.
More Information
This identity is a fundamental result in trigonometry that relates the tangent function to the cosine function, often used in solving various trigonometric equations and simplifying expressions.
Tips
- Misapplying the formulas: Ensure to use the correct double angle formulas when substituting.
- Forgetting to verify both sides: Always check if both sides simplify to an equivalent expression.
AI-generated content may contain errors. Please verify critical information