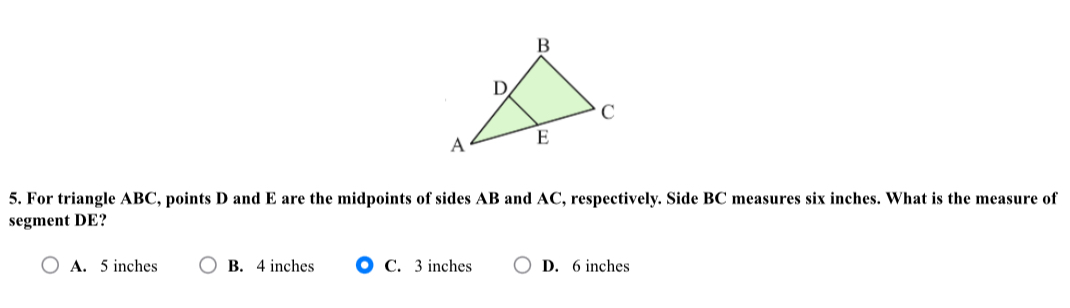
For triangle ABC, points D and E are the midpoints of sides AB and AC, respectively. Side BC measures six inches. What is the measure of segment DE?
Understand the Problem
The question describes a triangle ABC, where points D and E are midpoints of sides AB and AC, respectively. Given that side BC measures six inches, the question asks to find the length of segment DE. This involves applying the midpoint theorem, which states that the line segment connecting the midpoints of two sides of a triangle is parallel to the third side and half its length.
Answer
$DE = 3$ inches
Answer for screen readers
C. 3 inches
Steps to Solve
- Identify the Midpoints
The problem states that D and E are the midpoints of sides AB and AC, respectively.
- Apply the Midpoint Theorem
The Midpoint Theorem states that the segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length. Therefore DE is parallel to BC and $DE = \frac{1}{2}BC$.
- Calculate the length of DE
Given that BC = 6 inches, we can find DE:
$DE = \frac{1}{2} \times 6 = 3$ inches
C. 3 inches
More Information
The Midpoint Theorem is a special case of similar triangles. Triangle ADE is similar to triangle ABC, with a ratio of 1:2.
Tips
A common mistake is to assume DE is equal to BC or another arbitrary value without applying the Midpoint Theorem. Also, sometimes students might incorrectly calculate one half of the given length.
AI-generated content may contain errors. Please verify critical information