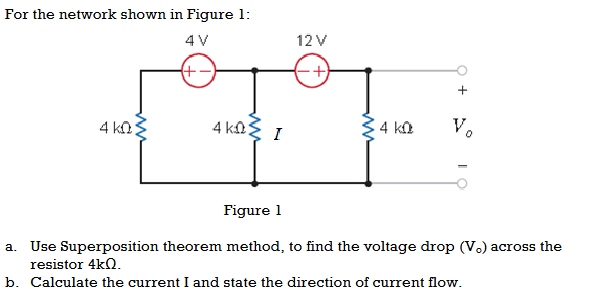
For the network shown in Figure 1: a. Use Superposition theorem method, to find the voltage drop (Vo) across the resistor 4kΩ. b. Calculate the current I and state the direction of... For the network shown in Figure 1: a. Use Superposition theorem method, to find the voltage drop (Vo) across the resistor 4kΩ. b. Calculate the current I and state the direction of current flow. Read more

Steps to Solve

1. Identify Individual Sources To apply the Superposition theorem, we need to analyze the circuit for each independent voltage source one at a time, while turning off the other sources. For voltage sources, we replace them with short circuits.

2. Analyze Circuit with 4V Source When considering the 4V source only:

• The circuit now has a 4V source and the two 4kΩ resistors in series.

• Find the current $I_1$ using Ohm's law. The equivalent resistance $R_{eq1}$ is $4kΩ + 4kΩ = 8kΩ$.

• The total voltage across this resistance is 4V. Thus,

  $$ I_1 = \frac{V}{R_{eq1}} = \frac{4V}{8kΩ} = 0.5 mA $$

3. Find Voltage Drop across the 4kΩ Resistor The voltage drop across the 4kΩ resistor due to the 4V source is:

$$ V_{4kΩ,1} = I_1 \cdot 4kΩ = 0.5mA \cdot 4kΩ = 2V $$

4. Analyze Circuit with 12V Source Now, only consider the 12V source:

• We have the 12V source and both 4kΩ resistors in parallel.
• The equivalent resistance $R_{eq2}$ is:

$$ R_{eq2} = \frac{(4kΩ \parallel 4kΩ)} + 4kΩ = 2kΩ + 4kΩ = 6kΩ $$

• The current $I_2$ through the circuit can be calculated as:

$$ I_2 = \frac{12V}{6kΩ} = 2mA $$

5. Find Voltage Drop across the 4kΩ Resistor The voltage drop across the 4kΩ resistor due to the 12V source is:

$$ V_{4kΩ,2} = \frac{(4kΩ \cdot 12V)}{(4kΩ + 4kΩ)} = \frac{4kΩ \cdot 12V}{8kΩ} = 6V $$

6. Add Voltage Drops for Total Voltage Now sum the voltage drops from both sources to find the total voltage drop $V_o$ across the 4kΩ resistor:

$$ V_o = V_{4kΩ,1} + V_{4kΩ,2} = 2V + 6V = 8V $$

7. Calculate Total Current and Direction The total current $I$ across the circuit is the same as the current $I_2$:

$$ I = I_2 = 2mA $$

Since the 12V source drives the current through the circuit, the direction of the current $I$ flows from the positive terminal of the 12V source towards the resistor.